| Support Topics | ||||
|
||||
| 卷首语 |
|
在Engineer's Studio® Ver 4.00.00当中追加了多点输入的功能。在本文当中将介绍多点输入与过往的地震波形输入的不同及注意事项。并在介绍过程中加入具体事例。 |
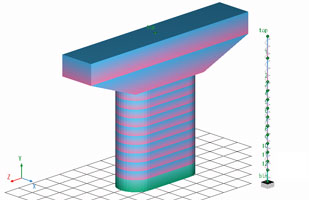
| 样本文件「MultiPointInput-RCPier.es」 |
|
装载Engineer's Studio®之后在文件夹当中会出现如上图的样本数据(图1)。这个模型是单柱普通钢筋混凝土桥梁的柱底部使用M-φ要素进行模型化的动力解析。 多点输入取得的变位是绝对变位,但因为现在是以取得相对变位为目的,柱下端的节点(全固定支点)和柱上端的节点(天端支 点)连接设置虚拟的弹性要素。因为是虚拟,弹性特性的6个成分都是「自由」的。这个弹性要素的结果就是柱下端对柱上端节点的相对位移。 设置有3个栏(一系列的解析)。
|
| 注意点1:多点输入和Rayleigh衰减 |
|
多点输入当中,时刻历强制变位的方法和时刻历加速度的两种方法的结果都可获得绝对变位。绝对变位不但包括构造物的变位还包 括地动自身的变位。 而在使用动力解析来计算质量比例性的减衰模子时地动变位及附加的衰减作用产生。其结果是,会取得与之前的相对变位的结果不 同的结果。 因此,质量比例型(α[K])与刚性比例型(β[K])的和使用Rayleigh衰减之后,当α不为0时,「地盘全体」的 结果(栏1)和「节点加速度」(栏2)的结果不一致。「节点强制变位」(栏3)也是一样。 若要使多点输入和以前的「地盘解析」取得同样的结果,必须采用刚性比例型衰减。即把Rayleighα设为0,只给与β有 意义的值或者根据要素不同进行刚性比例型衰减。 这个样品数据可根据要素的不通过来设定刚性比例型衰减。 |
| 注意点2:多点输入的「节点强制变位」 |
|
多 点输入的节点强制变位的波形形状必须另外进行解析在给予取得节点的时刻历变位。例如,在地盘解析的结果当中取得的节点的时刻历结果在多点输入中被当做多点 输入的强制变位来表示。 多 点输入的节点强制变位必须是波形形状在物理上成为可能才能做到。假如对其他解析结果不进行设置而只以试解析的方式输入(y=sin(x))的强制变位波形 后,会得到过大的应答加速度和反力。反力的结果会比取得必要以上的振动。这是在sin(x)微分时,因为是cos(x)、t=0最高速度。现实当中没有类似的波形。在样品数据当中,栏2取得的柱基部的时刻应答变位在线段3的节点强制变位当中使用(图4)。 |
| 注意点3:积分时间间隔 |
|
多点输入作为节点强制变位使用时,必须细分积分时间间隔。例如,「地盘全体」时积分时间间隔为0.01秒取得的解析结果相 同的精度取得必须使积分时间间隔为0.001秒。根据情况也会出现0.0005秒和0.0001秒等的细分情况。 这个理由是是假定变位分布为三次函数。三次函数当中根据时间的变化Δt的变位的变化量变大,因此必须把Δt缩小。 当样本数据的栏3当中因为M-φ要素的应答要素的应答剪断力是进行解的振动,在积分时间间隔为0.001s时,可以缩小 解的振动。但是只单纯细分积分时间间隔无法解决问题(后述)。 |
| 节点的应答 |
 ■图5 柱天端节点的时刻历应答图 诸线段节点的时刻历应答图如图5所示。栏1为相对变位,栏2与3是绝对变位。可以看到图中相对变位和绝对变位的不同。如上 所述绝对变位当中包含地动的变位。 |
| 弹性要素的应答 |
|
虚拟的弹性要素的时刻历如图6所示。栏1,栏2,栏3因为全部都是相对变位的量因此完全一致。栏2和栏3是除去 地动的变位,与栏1完全一致。  ■图6 模型弹性要素的时刻历应答图 |
| M-φ要素的剪切力 |
|
柱基部的M-φ要素的时刻历剪切力要素应答图如7所示。栏1(地盘整体)和栏2(节点加速度)虽然是一致的,但是栏3(节点强制变位)当中。这个理由与前述「注意点3」当中记载的一致。 在
这里积分时间间隔以0.001s来表示(如图8所示)与栏1,栏2,栏3完全一致。注意点为线段2的解析是以0.001s来进行,其结果可在栏3中
使用。也就是说,使用另计算的0.01s的结果,另使用积分时间间隔细分如0.001s例(如图8所示)与栏1,栏2,栏3的结果一致。并且栏2的解析以
0.001s进行,其结果在栏3中使用。也就是说,另外采用的0.01s的结果值使用积分时间间隔细分0.001s细分也无法取得良好的结
果。其原因是使用这个方法即使把精度提高输入波形的精度依然无法精准。  ■图7 柱基部的时刻历的剪切力应答图(Δt=0.01s)  ■图8 柱基部的时刻历剪切力应答图(Δt=0.001s) |
|
|||
| (Up&Coming '14 秋季号刊载) | |||
 |