(株)フォーラムエイト
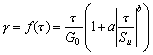
| γ | :Shear Strain | |
| τ | :Shear Stress | |
| γ0 | :Shear Strain at turning point | |
| τ0 | :Shear Stress at turning point | |
| G0 | :initial elastic shear stiffness | |
| b | :soil type factor (1.6 for sand,1.5 for sand and clay1.4 for clay) | |
| Su | :max. shear strength | |
| a | : |
HELPにある算定式より、まずN値からG0 を定め、そしてSu を決定しています。
| G0 | =11.76N0.8 |
| Su | =G0 / 600 for clay、G0 / 850 for sand and Clay、G0 / 1100 for sand |
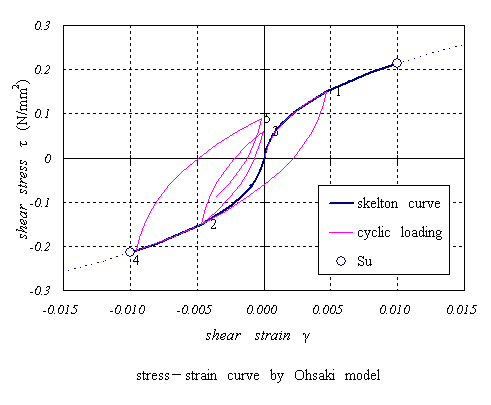
せん断ひずみが0.01をこえると、せん断剛性は極端に低くなり、地盤の塑性化を表現します。地盤反力度の上限値等を表現するためのものです。
 |
 |
|
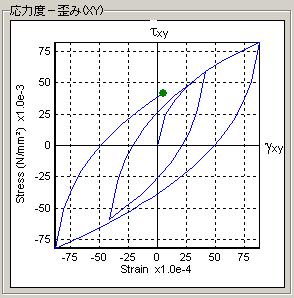
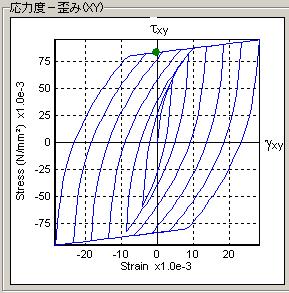
| 最大せん断ひずみ0.01以下 | 最大せん断ひずみ0.01以上 |
Shawky, A. and Maekawa, K. :Computational Approach to Path-Dependent Nonlinear RC/Soil Interaction, Proc. of JSCE, No.532/V-30, 1996.2
Shawky, A. and Maekawa, K. :Nonlinear Response of Underground RC Structures under Shear, Proc. of JSCE, No.538/V-31, 1996.5
OHSAKI, Y. :Dynamic Characteristics and One-Dimensional Linear Amplification Theories of Soil Deposits Research Report 82-01, Department of Architecture Faculity of Engineering University of Tokyo,1982.3
Ohsaki, Y. :Some notes on Masing's law and nonlinear response and soil deposits, Journal of the Faculity of Eng.(B),The University of Tokyo,Vol.XXXV,No.4,1980
| UC-win/WCOMD |