U&C Support Topics

Support Topics

Rigidity at eigen value analysis and frame reduction ratio

From Ver.10.0.0, elastic rigidity is used for M-φ eigen analysis, and the frame reduction ratio always becomes 1 or smaller when the reduction method is "Determination from M-φ". The differences from the old version are as below.

	Before Ver.9	After Ver.10
M-φ rigidity at eigen analysis	1st gradient of M-φ	Elastic rigidity (EI)
Reduction ratio when frame reduction is "Determination from M-φ"	・Less than 1 when trilinear ・Otherwise, 1.0	Always less than 1

The followings are the examples where the results of eigenvalue analysis match or do not match when reading a conventional data file.

Eigenvalue analysis results match

M-φ character of bilinear is assigned to the M-φ element (Fig.1).
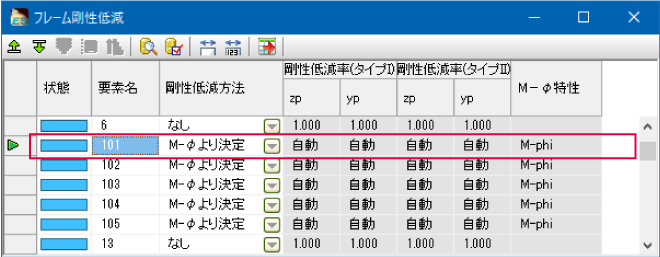
The reduction method of frame eigen analysis is "Determination from Mφ" (Fig.2).

In Ver.9, the frame reduction ratio is 1 and the 1st gradient of M-φ is used, which results in the yield stiffness. In Ver.10, the elastic rigidity is reduced (Fig.3). In both cases, the results of the eigenvalue analysis will be the same.

Fig.1 M-φ of bilinear

Fig.2 The reduction method of frame eigen analysis in Ver.9

Fig.3 The reduction method of frame eigen analysis in Ver.10

Example case of different eigenvalue analysis results 1

M-φ character of bilinear is assigned to the M-φ element (Fig.1).
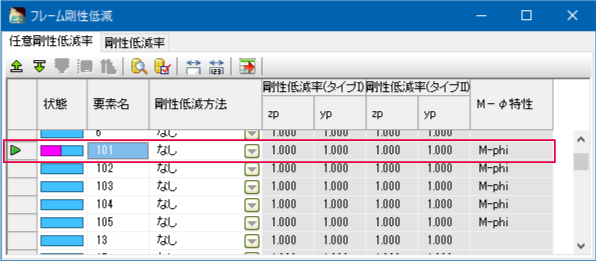
The reduction method of frame eigen analysis is "None" (Fig.4).

In Ver.9, the frame reduction ratio is 1 and the 1st gradient of M-φ is used, which results in the yield stiffness. In Ver.10, the elastic rigidity is used because the reduction method of frame is "None".
To match the results, change the reduction method to "Determination from Mφ" (Fig.5).

Fig.4 The reduction method of frame eigen analysis in Ver.9

Fig.5 Change the reduction method of frame eigen analysis in Ver.10

Example case of different eigenvalue analysis results 2

M-φ character of bilinear is assigned to the M-φ element (Fig.1).
The reduction method of frame eigen analysis is "Determination from Mφ" (Fig.6).

In Ver.9, the frame reduction ratio is 1.0 and the elastic stiffness is used. The ratio is less than 1.0 in Ver.10, and the yield rigidity is used.
To match the results, assign no M-φ to elastic beam or select "None" as the reduction method (Fig.7).

Fig.6 The reduction method of frame eigen analysis in Ver.9

Fig.7 Change the reduction method of frame eigen analysis to "None" in Ver.10

(Up&Coming '21 Summer issue)