|
用纖維元素將橋樑的柱子 yòng用 xiān纖 wéi維 yuán元 sù素 jiāng將 qiáo橋 liáng梁 de的 zhù柱 zi子 モデル化する際の指針 模型化時的指標 |
 |
| Support Topics | |||
| Support Topics、FEM / Engineer's Studio® | |||
|
|||
|
關於採用纖維要素的模型化,H29道路橋示方書的V編p.177表示「為了精確計算出鋼筋混凝土橋腳的終局水準耐力,將橋腳分割成鋼筋要素和混凝土要素,根據這些應力度-失真曲線進行非線性分析」被解說。可是,卻沒有提到具體的模型化方法。
guān關 yú於 cǎi采 yòng用 xiān纖 wéi維 yào要 sù素 de的 mó模 xíng型 huà化 , H 2 9 dào道 lù路 qiáo橋 shì示 fāng方 shū書 de的 V biān編 p . 1 7 7 biǎo表 shì示 「 wèi為 le了 jīng精 què確 jì計 suàn算 chū出 gāng鋼 jīn筋 hùn混 níng凝 tǔ土 qiáo橋 jiǎo腳 de的 zhōng終 jú局 shuǐ水 píng平 nài耐 lì力 , jiāng將 qiáo橋 jiǎo腳 fēn分 gē割 chéng成 gāng鋼 jīn筋 yào要 sù素 hé和 hùn混 níng凝 tǔ土 yào要 sù素 , gēn根 jù據 zhè這 xiē些 yīng應 lì力 dù度 - shī失 zhēn真 qū曲 xiàn線 jìn進 xíng行 fēi非 xiàn線 xìng性 fēn分 xī析 」 」 bèi被 jiě解 shuō說 。 kě可 shì是 , jù具 tǐ體 de的 mó模 xíng型 huà化 fāng方 fǎ法 méi沒 bèi被 chù觸 mō摸 。 そこで、國立研究開発法人土木研究所の土研資料第4262號「鉄筋コンクリート橋腳の地震時限界狀態の評価手法に関する研究」(平成25年3月)を參照します。當該資料にファイバー要素を用いた解析事例と具體的なモデル化方法が記載されています。ここでは、その解析事例を參考にした設定例を紹介いたします。 因此,參照國立研究開發法人土木研究所的土研資料第4262號「有關鋼筋混凝土橋腳的地震限制狀態的評價手法的研究」(2013年3月)。該資料中記載了使用光纖元素的分析事例和具體的模型化方法。在這裡,介紹一下參考了那個解析事例的設定例子。
zài在 nà那 lǐ裡 , cān參 zhào照 guó國 lì立 yán研 jiū究 kāi開 fā發 fǎ法 rén人 tǔ土 mù木 yán研 jiū究 suǒ所 de的 tǔ土 yán研 zī資 liào料 dì第 4 2 6 2 hào號 「 yǒu有 guān關 gāng鋼 jīn筋 hùn混 níng凝 tǔ土 qiáo橋 jiǎo腳 de的 dì地 zhèn震 xiàn限 zhì制 zhuàng狀 tài態 de的 píng評 jià價 shǒu手 fǎ法 de的 yán研 jiū究 」 ( píng平 chéng成 2 5 nián年 3 yuè月 ) 。 gāi該 zī資 liào料 zhōng中 jì記 zǎi載 le了 shǐ使 yòng用 guāng光 xiān纖 yuán元 sù素 de的 fēn分 xī析 shì事 lì例 hé和 jù具 tǐ體 de的 mó模 xíng型 huà化 fāng方 fǎ法 。 zài在 zhè這 lǐ裡 , jiè介 shào紹 yī一 xià下 cān參 kǎo考 le了 nà那 ge個 jiě解 xī析 shì事 lì例 de的 shè設 dìng定 lì例 zi子 。 圖1に示すように、単柱式鉄筋コンクリート橋腳に対して基部をファイバー要素とします。要素長は塑性ヒンジ長Lpとします。 如圖1所示,相對於單柱式鋼筋混凝土橋腳,基部作為纖維要素。元素長度為塑性鉸鏈長Lp。
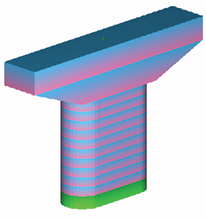 圖1橋柱模型
tú圖 1 qiáo橋 zhù柱 mó模 xíng型 ファイバー斷面は、コアコンクリート部(黒色部分)とかぶりコンクリート部(青色部分)に分けてメッシュ分割します(圖2)。 纖維斷面分為核心混凝土部分(黑色部分)和覆蓋混凝土部分(藍色部分)進行網狀分割(圖2)。 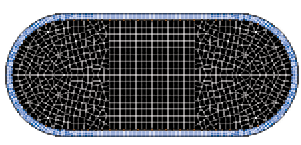 圖2光纖斷面網格分割 tú圖 2 guāng光 xiān纖 duàn斷 miàn面 wǎng網 gé格 fēn分 gē割 コアコンクリートの応力ひずみ曲線 核心混凝土應力失真曲線
hé核 xīn心 hùn混 níng凝 tǔ土 yìng應 lì力 shī失 zhēn真 qū曲 xiàn線 コアコンクリート部は橫拘束効果を考慮できますので、カテゴリを「Hoshikuma」とし、鉄筋による橫拘束効果を設定します(圖3)。 核心混凝土部因為能考慮橫(側)拘束效果,把類別作為「Hoshikuma」,設定由於鋼筋的橫(側)拘束效果(圖3)。 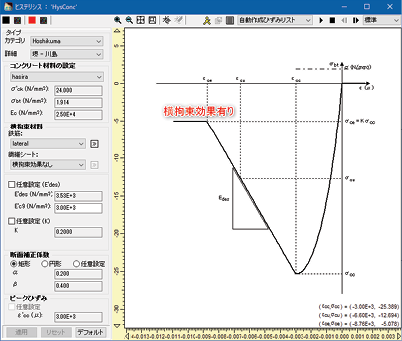
圖3核心混凝土的滯回性
tú圖 3 hé核 xīn心 hùn混 níng凝 tǔ土 de的 zhì滯 huí回 xìng性 かぶりコンクリートの応力ひずみ曲線 覆蓋混凝土的應力失真曲線
fù覆 gài蓋 hùn混 níng凝 tǔ土 de的 yìng應 lì力 shī失 zhēn真 qū曲 xiàn線 かぶりコンクリート部もカテゴリを「Hoshikuma」としますが、橫拘束筋がなく、橫拘束筋の體積比が0の場合、最大応力後の下降勾配を算出することができないという問題があります。そのため、土研資料第4262號では、橫拘束筋體積比を十分に小さな値として0.05%を入力して下降勾配を算出しています(圖4)。 蓋澆混凝土部份也把類別作為「Hoshikuma」,不過,有橫拘束肌,橫拘束肌的體積比是0的情況,不能算出最大應力後的下降梯度這樣的問題。為此,土研資料第4262號,作為充分小值輸入0.05%作為橫拘束肌體積比計算出下降梯度(圖4)。 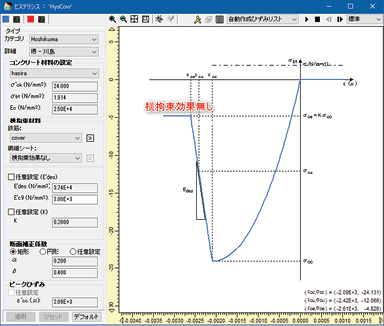
圖4覆蓋混凝土的滯回性
tú圖 4 fù覆 gài蓋 hùn混 níng凝 tǔ土 de的 zhì滯 huí回 xìng性 ここで、參考のためにコアコンクリートとかぶりコンクリートのヒステリシスを重ねて比較すると圖5のようになります。 這裡,為了參考核心混凝土和蓋混凝土的滯回性重疊比較的話,圖5變成那樣。
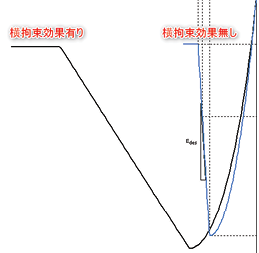 圖5覆蓋混凝土的滯回性
tú圖 5 fù覆 gài蓋 hùn混 níng凝 tǔ土 de的 zhì滯 huí回 xìng性 コファイバー要素のM-φ履歴応答 光纖元素的M-φ歷史回應
guāng光 xiān纖 yuán元 sù素 de的 M - φ lì曆 shǐ史 xiǎng響 yìng應 ファイバー要素のM-φ履歴応答を圖6に示します。比較のために、M-φ特性を緑線で表示しています。M-φ特性は、圧縮側のかぶりコンクリートの応力負擔を考えず、側方部分のかぶりコンクリートに橫拘束効果を考慮した応力ひずみ曲線を設定して算出されたものですので、ファイバー要素と條件が異なり、単純に比較できませんが、概ね一致していると言えます。 在圖6中示出纖維元素的M-φ歷史回應。為了比較,用綠色線表示著M-φ特性。M-φ特性是不考慮壓縮側的蓋澆混凝土的應力負擔,在側方部分的蓋澆混凝土上設定考慮了橫對。 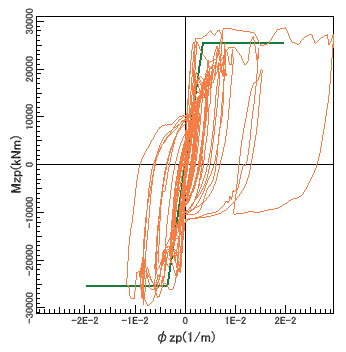 圖6 光纖元素的M-φ歷史回應 |
|
|||
| (Up&Coming '19 秋季號刊載) | |||
 |