| New Products |
|
|
|
「Engineer's Studio® を用いたイージーラーメン橋のレベル2地震動解析の紹介」 CPD認定
朝日エンヂニヤリング 株式会社 常務取締役 中井 良彰 氏
2011年11月17日(水)11:15〜12:00 会議室A
「Engineer's Studio®、UC-win/FRAME(3D)の最新機能と活用事例の紹介」 CPD認定
2011年11月17日(水)15:00〜15:30 会議室A |
|
|
Engineer's Studio®Ver 1.07の主な改訂項目は次の5点です。
- M-φ要素、M-θ特性の自動算出と照査
- 残留変位照査機能
- 固有値解析時の剛性低減
- 列車荷重「EA荷重」の牽引分布荷重入力
- ケーブル要素
|
道路橋などの地上構造物で、レベル2地震動に対して耐震設計を行う場合に、M-φ要素やM-θモデルを用いた動的解析が頻繁に実施されます。本版ではこれらの照査機能を追加しました。道路橋示方書V耐震設計編(以下、道示Vと呼ぶ)に準じて、M-φ特性やM-θ特性を自動的に算出し、それぞれに対して許容曲率や許容回転角で照査を行います。
図1は結果画面です。結果では許容値に対する応答値の比率、つまり安全率を一覧表示します。安全率が1.0を超えればNGとして赤く表示されます。すべての照査項目に比率が表示されるので、余裕のある設計となっているか、限界値ギリギリの設計になっているかが一目瞭然です。比率が厳しい順にソートする機能も搭載しています。
また、一部分の部材やばね要素をグループに登録しておけば、グループ毎に厳しい結果を表示する機能もあります。
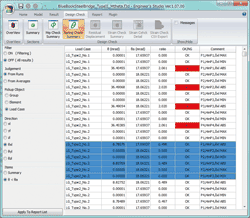
■図1 ばね要素(M-θ)の照査結果一覧
|
道示Vの「6.4.6 鉄筋コンクリート橋脚の照査」に準じた残留変位の照査を厳密に行います。橋梁全体系をモデル化して解析を行うと、橋脚天端節点の最大応答変位(全体系における絶対変位)には、基礎の回転による水平変位や基礎自身の水平変位が含まれています。本版では、これらを除去して橋脚躯体の変形量を抽出します。具体的には、図2に示すδprを自動算出します。
さらに、動的解析においては、各ステップごとにδprを逐次算出し、最大値を求めます。曲線橋や斜橋などの二軸曲げを受ける場合は、最大応答変位の方向に降伏変位を別途算出するなどの処理も行いますので、最大変位と降伏変位の方向が一致しないという問題もありません。
弊社製品UC-win/FRAME(3D)の残留変位照査機能には、上述の基礎による変位の含有、二軸曲げを受ける場合の不整合といった課題があります。本製品で大幅な改善を行いました。
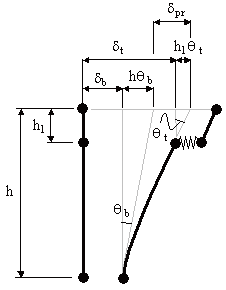 |
■図2 残留変位の照査式
δpr = δt +h1・θt -δb -h・θb
δpr :橋脚躯体の変形量
δt :橋脚天端の水平変位
δb :基礎底面の水平変位(※文献1では橋脚基部の変位とされています)
θt :橋脚天端の回転角
θb :基礎底面の回転角
h :基礎底面から上部構造慣性力作用位置までの高さ
h1 :橋脚天端から上部構造慣性力作用位置までの高さ |
|
固有値解析を行うときに部材やばね要素の剛性を低減することができます。道路橋ではレベル2地震動に対する耐震設計において、部材の降伏剛性を用いて固有周期を算定します。この機能を使うと、M-φ要素やばね要素を用いたM-θモデルの降伏剛性を自動算出させて固有値解析を行うことができます。
|
本製品には影響線解析を行う機能があります。連行荷重は、複数の集中荷重を移動させて断面力等が最大最小となる位置と結果を算出します。今回、集中荷重だけでなく分布荷重も考慮するようにしました。これにより、「鉄道構造物等設計標準・同解説
コンクリート構造物 平成16年4月」にある列車荷重「EA荷重」の牽引分布荷重を考慮できます。概念図を図3に示します。図中のA部(黄色)が牽引分布荷重です。B部は複数の軸重が一体となって移動します。
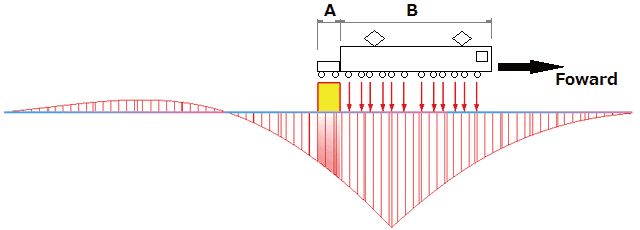
■図3 集中荷重と分布荷重を考慮した連行荷重
|
ケーブル要素は、引張だけに抵抗し、圧縮や曲げには抵抗しない構造要素です。ケーブルの両端を持って持ち上げると下に凸型の曲線の形になります。これを懸垂曲線またはカテナリーと呼ばれます。
本製品のケーブル要素は、カテナリーを定式化した要素です。材料パラメータとして、断面積A、ヤング係数E、ケーブル軸線に沿った単位長さ当たり質量mを与えます。ケーブルの形状を定めるために4通りの入力方法があります。それは、水平張力を与える方法、自然長を与える方法、自然長に対する最大サグを与える方法、水平方向任意位置でのサグを与える方法、のいずれかを用いて入力します。
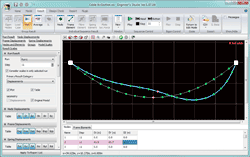
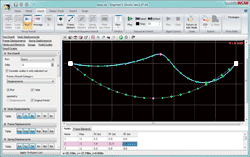
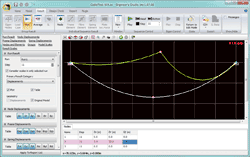
例として、E= 2.0E+05(N/mm2)、A=0.125(m2)、m=1000(kg/m)、水平張力H=490.3(kN)の条件を、従来の梁要素(微小変位と大変位)と新しいケーブル要素とで比較してみます。荷重条件を図4に示します。梁要素では曲げ剛性を小さくし、精度を高めるために10分割しています。ケーブル要素は2分割です。
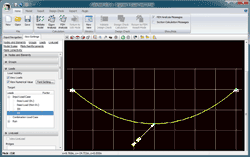
梁要素を微小変位理論で解析すると図5のように不自然な変形となります。大変位で解析すると図6のようにケーブルの挙動に近くなりますが、載荷点では梁要素特有の変形図になります。ケーブル要素を用いると2分割でも精度の高い結果が得られ、ケーブル特有のカテナリーを維持した変形が得られます(図7)。
動的解析ではケーブルの質量分布や減衰を精度よく考慮するために、ケーブルの分割が必要です。
 |
|
 |
■図4 ケーブル中央に上向き45度方向に
集中荷重載荷 |
|
■図5 「10個の梁要素+微小変位」の変位図 |
 |
|
 |
| ■図6 「10個の梁要素+大変位」の変位図 |
|
■図7 「2個のケーブル要素+大変位」の変位図 |
|
|






>> 製品総合カタログ
>> プレミアム会員サービス
>> ファイナンシャルサポート
|








