• 
  • TOP PAGE
• 
  • 新着情報
  • 開発情報
  • Up&Coming
  • キャンペーン情報
  • ポイント・バンク
  • プレスリリース
• 
  • コンテスト／協議会
  • 有償セミナー
  • 体験セミナー
  • イベント
  • セミナーレポート
  • セミナー・イベントカレンダー
• 
  • 製品情報：シリーズ別
    • UC-winシリーズ
      • シミュレーション
      • FEM解析
    • 3DCGシリーズ
    • UC-1シリーズ
      • 構造解析／断面
      • 橋梁上部工
      • 橋梁下部工
      • 基礎工
      • 仮設工
      • 道路土工
      • 港湾
      • 水工
      • 地盤解析
      • CALS／CAD
      • 維持管理・地震リスク
      • 建築／プラント
      • 船舶／避難
    • Suite/スイートシリーズ
    • サポート/サービス
  • 製品情報：ソリューション別
    • 耐震診断／補強
    • 鋼橋設計
    • 橋梁新工法
    • 建築設計
    • 自治体
    • ECO
  • 新製品／バージョンアップ情報
  • 開発中製品情報
  • 受託開発サービス
  • Products Guide製品カタログ
  • 電子マニュアル・操作ガイダンス
• 
  • オーダーページ（製品購入／御見積作成）
  • レンタルライセンス／フローティングライセンス
  • WEB見積サービス　
  • 資料請求
• 
  • 製品別サポート
  • 動作環境一覧表
  • 問合フォーム
  • ユーザ情報ページ
  • 電子メールサービス
• 
  • 特許一覧
  • 商標一覧
  • メディアでの紹介／記事・広告掲載
  • 協賛・スポンサー／パートナー
  • リンク集
  • 論文発表
  • WebLesson
  • リンク集
• 
  • 会社案内
  • 採用情報
  • 決算公告
  • Branch&Showroom (支社一覧)
  • お問い合わせ
  • 海外代理店

Mighty Bridge Ｑ＆Ａ

４．柱トラス断面計算

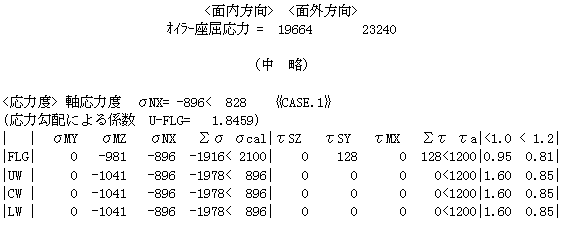
Ｑ４−１．	応力度の合計値Σσの値がそれぞれを加算した値に合わない 応力度表で曲げと軸力による応力度の合計Σσの値が、合計した値にならない。
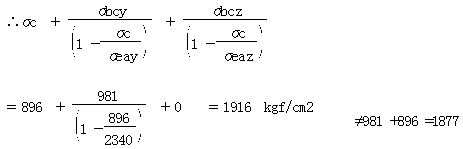
Ａ４−１．	道示�U−３.３軸方向と曲げを受ける部材の照査を行ってその結果のみを印字しているために、応力度の合計が一致しません。　 上記例の上フランジでは、 σc σbcy σbcz σeay σeaz ＝　　８９６kgf/cm2（圧縮） ＝　　９８１kgf/cm2（面外方向Ｍによる応力） ＝　　　　０kgf/cm2（面内方向Ｍによる応力） ＝２３２４０kgf/cm2（面外オイラー座屈応力） ＝１９６６４kgf/cm2（面内オイラー座屈応力） となります。
Ｑ４−２．	「押さえ方法」と「押さえ寸法」の入力 入力項目で「押さえ方法」と「押さえ寸法」について教えて下さい。
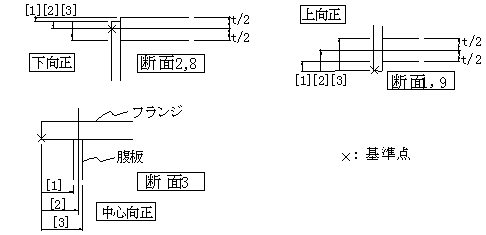
Ａ４−２．	断面形状タイプとして1〜10がありますが、フランジ幅や腹板高,板厚といった入力値では寸法の決まらない箇所の寸法を入力する項目です。入力の必要な断面タイプは、上フランジは2と8、下フランジは1と9、腹板は5です。 断面2,8（上フランジ）→腹板上端から上フランジのどの線に着目するかを「押さえ方法」で指定し、その寸法を「押さえ寸法」で入力する。 断面1,9（下フランジ）→腹板下端から下フランジのどの線に着目するかを「押さえ方法」で指定し、その寸法を「押さえ寸法」で入力する。 断面 3 （　腹　板　）→上フランジ端から腹板のどの線に着目するかを「押さえ方法」で指定し、その寸法を「押さえ寸法」で入力する。
Ｑ４−３．	「軸力部材か」の意味 入力項目で「軸力部材か」がありますが、この意味を教えて下さい。
Ａ４−３．	断面計算での腹板の扱いについて以下の様になります。 Ｙの時 腹板を道示�U-3.2圧縮応力を受ける板および補剛板として扱います。「片側補剛数」で入力した値のリブを腹板高に対し均等に配置し、腹板の許容応力度とリブの必要剛度照査を行います。 Ｎの時 腹板をプレートガーダーの腹板として扱い、「横補剛高厚」で入力した水平補剛材を「水平段数」分設置し腹板の必要板厚を道示�U-8.4、補剛材間隔照査を道示�U-8.4等で行います。
Ｑ４−４．	計算結果の必要板厚と許容応力度の算定 必要板厚と許容応力度の算出について、例を挙げて説明して下さい。
Ａ４−４．	各荷重ケース毎に上下フランジは左右端、腹板は上下端での応力度の合計を求め応力状況を調べる。 両端とも［引張］と判断された場合 　　 ・許容応力度は、道示�U-3.2.1（表-2.2.1） による ・必要板厚は、 道示�U-8.3.1もしくは8.3.2による 両端とも［圧縮］と判断された場合 ・ 許容応力度は、道示-3.2.1及び3.2.2及び3.2.3による ・ 必要板厚は、各許容応力度表（表-3.2.2、表3.2.3、表3.2.5）の中の板厚境を採用しています。また、両端支持板と両端を支持された補剛板の時は同時に（表-3.2.1）（表-3.2.4）も考慮して、許容応力度表の板厚境の値と比較し大きくなった方を採用しています。 片側［圧縮］、片側［引張］の場合 　両端とも［圧縮］の時と同じです。 面外曲げ［ＭZ］が作用したときの腹板について フランジについては上下別々に印字していますのでよいのですが、箱断面の場合にはどちらか片側しか印字していません。但し、内部計算では［ＭZ］による腹板の実応力が全圧縮になる場合と、全引張になる場合（つまり左側腹板と右側腹板という意味）の両ケースを照査して、必要板厚及び許容応力度ともどちらか危険側を採用しています。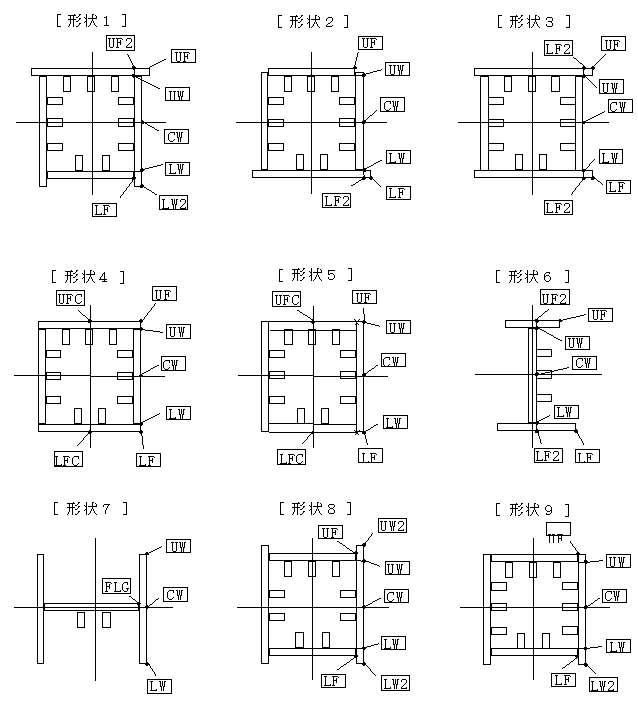 以下に断面形状［５］について手計算で追います。 Mighty-Bridge�@柱断面計算 　　応力度着目位置
Ｑ４−５．	曲げと軸力を受ける部材の合成応力度の算出 計算結果の項目で、道示�U-3.3軸方向と曲げモーメントを受ける部材の照査を行っていますが、他社の結果と少し違っています。本プログラムではどの様に計算しているか例を挙げて解説して下さい。
Ａ４−５．	御問い合わせ件ですが、結論から申しますと一概に本プログラムがおかしいとも思えず計算方法に違いがあるためと思われます。それは以下の点です。 �@σcaz算出時のσcalの取り方で、本プログラムでは着目点が上フランジ、腹板、下フランジと分かれているので、上下フランジは道示（3.2.2）腹板は（3.2.3）により求めている。これに対し他社は危険側となる腹板だけしか考えていない。 �A曲げによる応力度（σbcy）も本プログラムでは着目点が分かれているので、それぞれ採用しているが、他社が腹板上縁がなくフランジ端のみを考えている。 �Bつまり 　ＭＢ　→　上下フランジ縁の断面力と道示（3.2.2）フランジによるσcal、Web縁の断面力と道示（3.2.3）腹板によるσcalとそれぞれ組み合わせて照査。 　他社　→　上下フランジ縁の断面力とWeb縁道示（3.2.3）腹板によるσcalを組み合わせて照査します。他社のプログラムでは、着目する箇所を本プログラムの様に設けていないためこ思います。この様な組み合わせで照査しているものと思われます。どちらが正解かは分かりませんが、本プログラムの方法も特に間違いとは言えないと次のページに頂きました本プログラム出力の《CASE.1》を着目点別 UF UW LW LFに手で追った資料を添付します。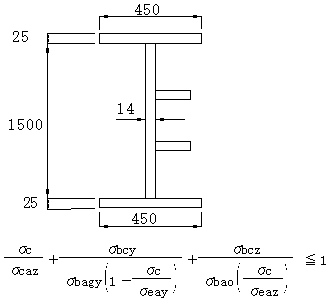 上フランジ：ＵＦ １）σc＝560kgf／cm2（圧縮） ２）σcaz＝弱軸のまわりの許容軸方向 　　　　　 ＝σcag×σcal／σcao 　ここに�@σcagは、ｌ／ｒ＝38.68（弱軸）より 　　　　　　σcag＝2100−15(38.68−14) 　　　　　　　　　 ＝1729.8　kgf／cm2 　　　　　�Aσcalはフランジなので(3.2.2)より b＝ (45−0.9) 　　　　　　 ２ ＝22.05 b 　　　 10.7 　22.05 ＝　　　　 　10.7 ＝2.06＜2.5 ∴σcal＝2100kgf／cm2 　　　　　�Bσcao＝2100kgf／cm2 ゆえに　　σcaz＝1729.8×2100／2100＝1729.8kgf／cm2 ３）σbcy＝強軸まわりに作用するＭによる曲げ応力 　　　　　 ＝152kgf／cm2 ４）σbagy＝局部座屈を考慮しない許容曲げ圧縮応力度 　　　　　　　（表-2.2.2） ＝ / 　 b 　361.5 ＝　　　　 　45 ＝8.03＞3.5 ∴σbagy＝2100−44(8.03−3.5)＝1900.7kgf／cm2 ５）σeay＝359288kgf／cm2（強軸オイラー印字より） ６）１）〜５）より 腹板上縁：ＵＦ 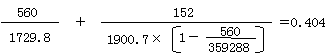１）σc＝560kgf／cm2 ２）σcaz 　�@σcag＝1729.8　kgf／cm2 　�Aσcalは(3.2.3補剛板）より ３）σbcy＝147　kgf／cm2 ４）σbagy＝1900.7　kgf／cm2 ５）σeay　＝359288　kgf／cm2 ６）１）〜５）より 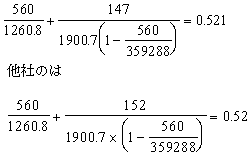σｂｃｚにフランジ上縁の応力度を用いている。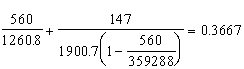 腹板中央：ＣＷ 560 　　　　 1260.8 +0＝0.441 腹板下縁：ＬＷ σbcyが引張（−）になるだけなので 下フランジ：ＬＦ １）σc＝560kgf／cm2（圧縮） ２）σcaz　　�@σcag＝1729.8／cm2 　　　　　　　�Aσcalはフランジなので(3.2.2)より 　　　　　　　 b＝ (45-0.9) 　　　　　 2 ＝22.05cm 　b 　　　＝ 10.7 22.05 　　　　 10.7 ＝2.06＜2.5 　　　　　　　∴σcao＝2100　kgf／cm2 　　　　　　　�Bσcao＝2100　kgf／cm2 　　　　　　　∴σcaz＝1729.8×2100／2100＝1729.8　kgf／cm2 ３）σbcy＝−152.0　kgf／cm2（引張） ４）σbagy＝1900.7　kgf／cm2 ５）σeay＝359288　kgf／cm2 ６）１）〜５）より
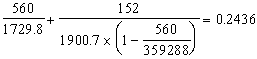Ｑ４−６．	断面タイプ�T断面の補剛材の照査について 断面タイプ�Tで、[軸力部材＝Ｙ]として腹板に補剛板を設置しました。この時の補剛材の照査について説明して下さい。
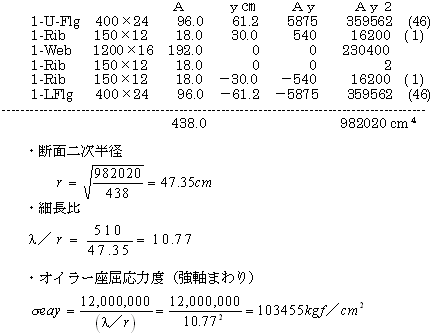
Ａ４−６．	「軸力部材か」のスイッチで影響する内容は、腹板の扱い方です。腹板の必要板厚や局部座屈による許容応力度、補剛材の必要剛度等が変わってきます。簡単にまとめると以下の通りです。 断面形状＝６：Ｉ断面の例 軸力部材か Ｙの時 Ｎの時 腹板の必要板厚 �U-3.2圧縮応力を受ける板 および補剛板により算出 �U-8.4プレートガーダの腹板 表-8.4.1により算出 腹板の局部座屈による 許容応力度 �U-3.2により算出 全　強 補剛材の照査 必要断面二次モーメント �U-3.2.4式（3.2.3）により算出 �U-8.6.2式（8.6.1）により算出 1）断面諸量 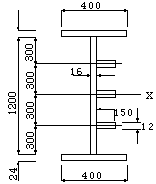Ｍ＝-213.1 tf･m Ｓ＝ 52.3 tf Ｎ＝ -63.1 tf 面外座屈長＝5.100 m 面内　〃 ＝5.100 m 面内方向 面外方向 Ａ ｙ�p Ａｙ Ａｙ2 2-U-Flg 400×24 192.0 0.0 0.0 25600 1-Web 1200×16 192.0 0.0 0.0 41 3-Rib 150×12 54.0 8.3 448 3720 (1013) 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 438.0 30374 cm4 e＝0としている ・断面二次半径 ・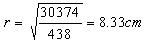細長比 λ／r＝ 510 　　　 8.33 ＝61.24 ・オイラー座屈応力度（弱軸まわり） 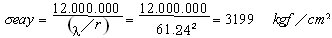２）腹板に付くリブの照査 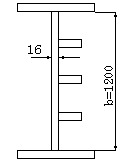断面−３−ＰＬ150×12(18.0cm2) 横リブ間隔 a＝127.5 �p パネル数n＝ 4 縦リブ断面積 �U-2.3.4 (3.2.4)式 bt 　　＝ 10n 120×1.6 　　　　　　 10×4 ＝4.8cm2≦15×1.2 縦リブ剛度 �U-2.3.4 (3.2.4)式 横方向リブの必要剛度 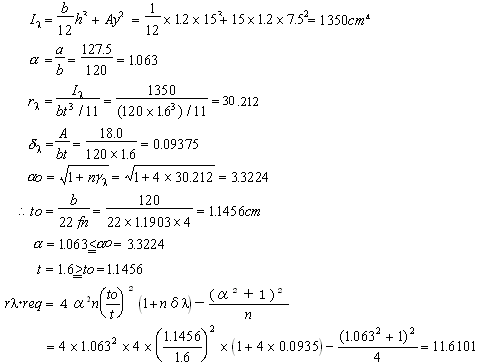Ｉt･req＝ bt3 　　× 11 1＋n×rλ･req 　　　　　　　　　＝ 　　　4α3 1 　　×120×1.63× 11 （1+4×11.6101） 　　　　　　　　　　 4×1.0633 441cm4 縦方向リブの必要剛度 Ｉt･req＝ bt3 　　×rλ･req＝ 11 1 　　×120×1.63×11.6101＝518cm4 11

Mighty Bridge　インデックス