| Q4-8. |
断面タイプ5で有効幅係数を入力した時
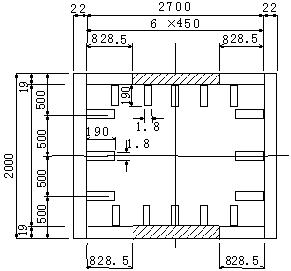
断面タイプ5で有効幅を低減したいため「面内幅係数」として下図の様に入力しました。この時の出力される断面二次モーメントの値は、どの様に算出していますか?
柱トラスで有効幅係数を入力した時
|
有効幅係数
と入力。 |
|
| A4-8. |
本プログラムで幅係数を入力すると、フランジ及びリブの断面積に入力した係数を乗ずるだけです。フランジの場合はよいのですが、リブの場合はフランジリブ全断面積に幅係数を乗じた断面積となり、フランジの有効幅とリブ配置から何本が有効幅内にあるのか....という判断は行っていません。このための断面積の差が原因です。
フランジ有効断面積=腹板中心間隔×幅係数×板厚
リ ブ 有効断面積=リブ幅×リブ高×幅係数×本数
| |
A |
y㎝ |
Ay2 |
I |
| U.FLG 270×1.9 |
513×0.614=315.0 |
99.05 |
G 5032993
N 3090434 |
154
95 |
| U.RIB 5×19×1.8 |
171.0×0.614=105.0 |
88.6 |
G 1342343
N 824246 |
5144
3158 |
| WEB 2×200×2.2 |
880.0 |
0.0 |
0 |
2933333 |
| WEBRIB1 2×19×1.8 |
68.4 |
50.0 |
171000 |
18 |
| WEBRIB2 2×19×1.8 |
68.4 |
0.0 |
0 |
18 |
| WEBRIB2 2×19×1.8 |
68.4 |
-50.0 |
171000 |
18 |
| L.RIB 5×19×1.8 |
171.0×0.614=105.0 |
-88.6 |
G 1342343
N 824246 |
5144
3158 |
| L.FLG 270×1.9 |
513×0.614=315.0 |
-99.05 |
G 5032993
N 3090434 |
154
95 |
|
G 2453.2 |
|
G 16036655 |
| N 1925.2 |
|
N 11111253 |
 |
| Q4-9. |
断面計算照査項目の意味
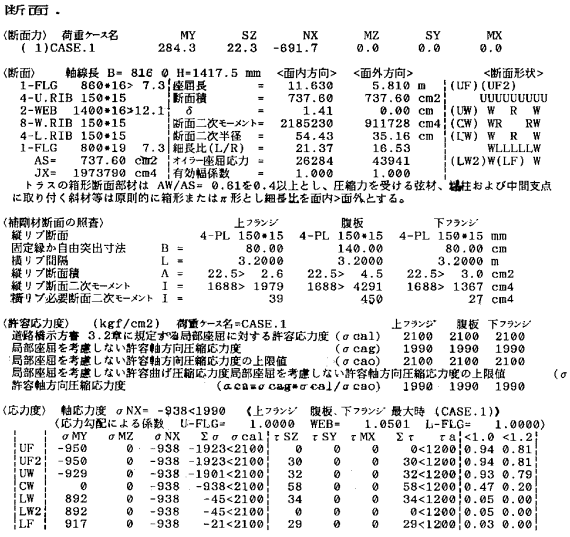
柱トラスアーチ部材の断面計算で出力される照査項目について、それら項目の意味を解説して下さい。 |
|
- 1)圧縮フランジ
- 道示Ⅱ-3.2圧縮応力を受ける板および補剛板に示される、許容応力度表の板厚境を必要板厚としています。
- 2)引張フランジ
- 道示Ⅱ-8.3.1及び8.3.2により決定。
- 3)腹板
- 入力項目の内
・軸力部材か Yの時→圧縮フランジと同様。
・軸力部材か Nの時→道示Ⅱ-8.4、表-8.4.1により決定
圧縮応力を生ずる、上下フランジ及び腹板について、道示Ⅱ-3.2.4により補剛材の照査を行います。
但し、入力項目の「軸力部材か」をNにするとプレートガーダの腹板とみなし、腹板の補剛材照査は行いません。
- 1)縦リブ必要断面積
- 式(3.2.4)により算出
- 2)縦リブ必要断面二次モーメント
- 式(3.2.3)により算出
- 3)横リブ必要断面二次モーメント
- 式(3.2.6)により算出
- 4)垂直補剛材の間隔照査(軸力部材か=Nの時)
- 道示Ⅱ-8.5.1(2)により照査
- 1)σMY :面内曲げモーメント(MY)による実応力度
-
- 2)σMZ :面外曲げモーメント(MZ)による実応力度
-
- 3)σNX :軸力(NX)による実応力度
-
- 4)Σσ :道示Ⅱ-3.3、軸方向と曲げモーメントを受ける部材の照査結果。
- 引張の時→(3.3.3)式
圧縮の時→(3.3.5)式
- 5)σcal:道示Ⅱ-3.2に示す、局部座屈に対する許容応力度
6)τSZ :面内せん断力(SZ)による実せん断応力度
- せん断流理論により算出。道示Ⅱ-図解8.2.1
- 7)τSY :面外せん断力(SY)による実せん断応力度
8)τMY :ねじりモーメント(MX)によるねじりせん断応力度
9) Στ:せん断応力度 合計(τSZ+τSY+τMX)
10) τa :許容せん断応力度
11)<1.0道示Ⅱ-3.3の安定照査
- 引張の時→(3.2.2)式
圧縮の時→(3.3.4)式
- 12)>1.2道示Ⅱ-8.2.4の合成応力度の照査
 |
| Q4-10. |
Ⅰ断面腹板のせん断力
I断面形状で、せん断応力度の算出方法を解説して下さい。 |
| A4-10. |
次ページの計算例についてまとめます。
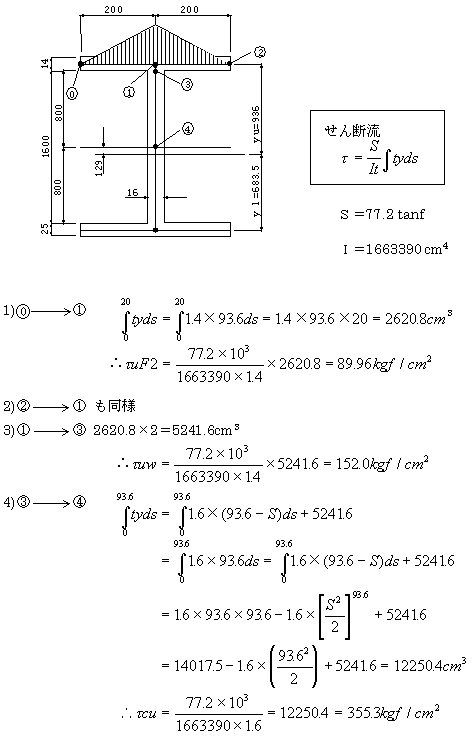 |
| Q4-11. |
Ⅰ断面全圧縮時許容応力と板厚
I桁断面計算で、全圧縮時の腹板許容圧縮応力度と必要板厚の算定方法について教えて下さい。 |
| A4-11. |
- 1.局部座屈による許容応力度(道示Ⅱ-3.2)
- ①応力状態より上下フランジとも圧縮。
道示Ⅱ-3.2.2より
| b = |
30.0-1.0
2 |
=14.5cm |
b
=
13.1 |
14.5
=
13.1 |
1.11cm<使用板厚1.3cm |
ゆえに σcal = 1400 kgf/cm2
②腹板(補剛材1段 n=2)
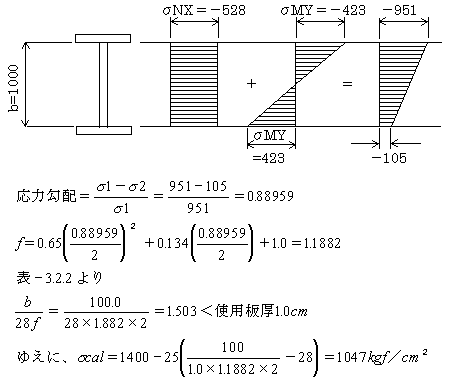
- 2.全体座屈による許容応力度(道示Ⅱ-2.2.2)
- 上下フランジ腹板とも
| l/r= |
300.0
5.74 |
=52.26>20 |
ゆえに σcag=1400-8.4(52.26-20)
=1129 kgf/cm2
- 3.局部座屈を考慮しない許容曲げ圧縮応力度(σbagy)
- 表-2.2.3(b)より
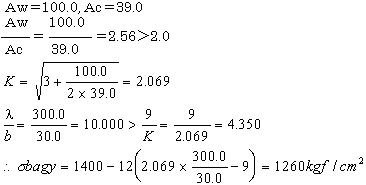
4.許容軸方向圧縮応力度(σca)
道示Ⅱ-2.2(2.2.1)式より
- ①上下フランジ σcao(上限値)は1400
σca=
= |
σcag×σcal/σcao
1129×1400/1400=1129 kgf/cm2 |
②腹板
| σca=1129×1047/8400= |
844 kgf/cm2 |
|
これがWEBのσcaとなる |
- 5.腹板の必要板厚
- 表-3.2.4か表3.2.5板厚境の大きい方を採用している。
| 表-3.2.4より |
b
=
56fn |
100.0
56×1.1882×2 |
=0.75 ←こっち |
| 表-3.2.5より |
b
=
80fn |
100.0
80×1.1882×2 |
=0.53 |
0.53 以上、bが大きくσcalが小さくなっているためσcも小さくなる。
|
| Q4-12. |
断面タイプ3で有効幅係数を入力した時
断面タイプ3で、面内幅係数を入力しました。この時断面二次モーメントはどの様に計算していますか? |
| A4-12. |
張出部のある断面タイプで幅係数を入力した場合、フランジとリブの断面積を以下の様に算出しています。
・フランジ有効断面積=(2×張出長+腹板中心間隔×幅係数)×板厚
・リブ有効断面積 =(リブ幅×リブ高×幅係数)×本数 |
| Q4-13. |
腹板に付くリブの必要剛度がマイナス
柱トラス断面計算で、「軸力部材か=Y」の時の服板に付くリブの必要断面二次モーメントが負の値で出力されます。 |
| A4-13. |
断面力のうち軸力が引張となり、腹板上下縁の応力バランスが引張が支配的となり、応力勾配が大きくなるため、この様な結果となっています。計算課程としては、正しく行われています。
次の計算例を手計算してみると
1)腹板の応力勾配
腹板上縁=-1046+794=-252(圧縮)
腹板下縁= 1046+794= 1840(引張)
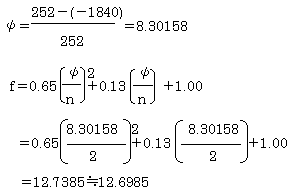
2)縦リブの必要断面積
道示Ⅱ-3.2.4 式(3.2.4)より
| Areq= |
bt
=
10n |
100×1.0
=5.0cm2>11.0×1.01=1.0cm2
10×2 |
3)縦リブの必要断面二次モーメント
道示Ⅱ-3.2.4より
使用縦リブの断面2次モーメント


 |