| �p�V�|�@�P�D |
���ׂ�̌v�Z�͈͂ɂ��āB |
| �`�V�|�@�P�D |
����ʂ̎n�_����I�_�܂ł��v�Z�͈͂ƂȂ�܂��B
�A���P�~���ׂ�̏ꍇ�̂��A�ȉ��̏����ƂȂ��Ă��܂��B
�~�̒��S�_����������������Ɗ���ʂƂ̌�_�����̊���ʁi�~�̒��S������������a���n�\�ʂƌ����ꍇ�A�~�̒��S�x���W����_�̂x���W�̕����傫�������̊���ʁj�͉����ʂƂ��Čv�Z���܂��B�Ȃ��A�����ʂɂ��Ă͒�R�i�b�A�Ӂj�����܂��B |
| �@ |
|
| �p�V�|�@�Q�D |
�n�w�u���b�N�̕������@�A�u���b�N�ԍ��̂ӂ���B |
| �`�V�| �Q�D |
�ȉ��̂悤�ɕ������������Ă��܂��B
- �n�\�ʌ`��ɉ����ċ��ܓ_���ɒ�̂��c����ɂ��܂��B
- �e�c����Ԃ̐��������������Ƃ��A�ѕЊ�����������ŏ������l�̐�グ�����A���̋�Ԃ̕��������ƂȂ�܂��B
�i���������^�����j�@
- �v�Z��̕������́A�u�����^���v�ƂȂ�܂��B
- �u���b�N�ԍ��̂ӂ���͂��ׂ�`��A���ׂ�����i���v���A�����v���j�Ɋւ�炸�A��ʌ������č�����u123n�v�Ƃ��Ă��܂��B
|
| �@ |
|
| �p�V�|�@�R�D |
�u���̎戵���v�ɂ��āB |
| �`�V�|�@�R�D |
- �������[�����g�v�Z�p
���ʂ���F��Ƀ����i�s�O�a�y�̒P�ʑ̐Ϗd�ʁj��p���܂��B
���ʂ�艺�F��Ƀ�sat�i�O�a�y�̒P�ʑ̐Ϗd�ʁj��p���܂��B
- ��R���[�����g�v�Z�p
���ʏ�ԂɊւ�炸�A�ȉ��̂T�p�^�[���̑g�ݍ��킹��C�ӂɑI���ł��܂��B
|
�P�ʑ̐Ϗd�ʃ� |
�Ԍ������� |
| �P�D |
�����i���͒l�j |
�O�D�O�Ƃ���B |
| �Q�D |
��sat�i���͒l�j |
�O�D�O�Ƃ���B |
| �R�D |
��'�i���͒l�j |
�O�D�O�Ƃ���B |
| �S�D |
��sat�|��w�@ |
�O�D�O�Ƃ���B |
| �T�D |
��sat�i���͒l�j |
�v�@�Z |
�i�ݒ��́u���̎�舵���v�Q�Ɓj
|
| �@ |
|
| �p�V�|�@�S�D |
�펞�A�n�k���̌v�Z���ɍs���邩�B |
| �`�V�|�@�S�D |
�����ɂ͍s���܂���B
�펞�����̏ꍇ�́u�v�Z���@�̐ݒ�v�ɂ����Đv�k�x�u�jH�A�jV�v�Ɂu0.0�v����͂��Ă��������B
�n�k�������̏ꍇ�́u�v�Z���@�̐ݒ�v�ɂ����Đv�k�x�u�jH�A�jV�v����͂��܂��B�X�ɖ{�v���O�����ł͂��̐v�k�x�u�jH�A�jV�v�Ɋe�w���Ƃɓ��͂�����W�������悶�Ă��܂��B�e�w���Ƃɐk�x��ύX�������ꍇ�ȂǂɃ���ς��ē��͂��Ă��������B���ɕύX���Ȃ��ꍇ�́u��=1.0�v�œ��͂��Ă��������B |
| �@ |
|
| �p�V�|�@�T�D |
��u ���O�@�̈����B |
| �`�V�|�@�T�D |
�v���O�����̏����Ƃ��ẮA�u���ʐ��v�ȉ��̃ӂ��O�Z�b�g���܂��B
�u���ʋ}�~�����v�Łu�����ʐ��v�Ɓu���ʐ��v������ꍇ�u���ʐ��v�ȉ��̃ӂ��O�Z�b�g���܂��B�]���āu���y����v�̂悤�ɐ��ʐ��̓��͂��s�v�ȏꍇ�ŁA�Ӂ��O�Ƃ��Čv�Z�������ꍇ�́A�\�ߓy���f�[�^�ŃӁ��O�Ɠ��͂��ĉ������B
�Q�l�j
�@�w�y���H�w�n���h�u�b�N�x�ɂ͎��̂悤�ɋL�q����Ă��܂��B
�u�S���͉�͖@�͉d�̕ω��₹��f�ɔ����Ĕ�������Ԍ������̗\��������ȏꍇ�ɗp�������͖@�ł���A�ʂɂ�u�@�܂��̓�u��0�@�ƌĂ��B�s�O�a�y�ł͂��ׂ�ʏ�̂����A���̓_�̃Ђ�p����
�@�@�@������u�{��tan��u�@�@�@�@�i�V�D�Q�j �@
�ŕ\�����Ƃ���B�����ɂ�u�A��u�͑S���͂Ɋւ��錩�����̔S���͂Ƃ���f��R�p�ł���A����Ɠ������x��ܐ���̋����̂ɑ��āA����Ɠ������x��ܐ���̋����̂ɑ��Ĕ���r�������i�t�t�����j���s���ċ��߂���B�s�O�a�y�̂t�t�����ł͍S�����̑傫���ɉ����ĊԌ���C�̈��k���N����A�O�a�y���ω�����̂ŕ���͒����ɂȂ�Ȃ��B�i�����j�O�a�y�ł͔�r���������O�͂ɂ�炸���Ŕj�����������i��u��0�j�ɂȂ邩��A���i�V�D�Q�j�́@
�@�@�@������u
�ƂȂ�B���ꂪ��u��0�@�ł���B�v
�@�@�����ɁA�@���@�F���ׂ�ʂŔ�������邹��f����
�@�@�@�@�@�@�@�bu �F��r������
�@�@�@�@�@�@�i�r�T�V�w�y���H�w�n���h�u�b�N�x�y���H�w��@P226�Q�Ɓj
�@ �܂��u�y�H�w�j�v�ɂ͎��̂悤�ɋL�q����Ă��܂��B
�u�펞�̎{�H����̐��y�̈���v�Z��S���͖@�ōs���ꍇ�A���y�ޗ����ח��y�œ��������Ⴂ�Ƃ��͔���r�������i�t�t�j��苁�߂����x�萔��u�A��u��p����B
�Ȃ��A��u�A��u�̂����Ɉꎲ���k������u��p���Ă�u��1/2��u�A��u=0�Ƃ��邱�Ƃ�����B�v
�@�@�@�i�r�U�Q�w���H�y�H�[�̂�ʍH�@�Ζʈ���H�w�j�xP151�Q�ƁB�j�@�@�@ |
| �@ |
|
| �p�V�|�@�U�D |
����X���C�X�ɕ����̑w�����݂����ꍇ�A�y���f�[�^�̎擾�͂ǂ̂悤�Ɉ����邩�B |
| �`�V�|�@�U�D |
���ꂼ��̊��蒷�̒������̓y���f�[�^�i���A�b�A�ӂȂǁj���擾���Čv�Z���܂��B�n�w���c����œ���X���C�X�ɕ������݂����ꍇ�����l�̈����Ōv�Z���܂��B |
| �@ |
|
| �p�V�|�@�V�D |
����ʂ��u�C�Ӑ܂���v�ŁA���̔C�Ӑ����u�n�w���v�ƈ�v�����ꍇ�A�y���f�[�^�̎擾�͂ǂ̂悤�Ɉ����邩�B |
| �`�V�|�@�V�D |
�C�Ӑ��ƒn�w������v�����ꍇ�͒���̓y���f�[�^���擾���Čv�Z���܂��B |
| �@ |
|
| �p�V�|�@�W�D |
�R�|�J�|�R�ꊊ��ʂ������ꍇ�̈����B |
| �`�V�|�@�W�D |
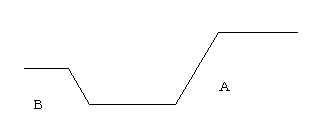
���ꂩ���蒷�̒������̎R���i�`�j�݂̂��擾���Čv�Z���A�����͖������܂��B
�]���Ċ��蒷�̒Z�����̎R���i�a�j�Ɂu�}�X�g�J�b�g���C���v��u�}�X�g�J�b�g�|�C���g�v���w�肵�Ă��Ă���������܂��B
�t�ɏ�}�̏ꍇ�Łi�a�j�݂̂�肽���ꍇ�́i�`�j���u�l�o�[�J�b�g���C���v���`���ĉ������B
|
| �@ |
|
| �p�V�|�X�D |
�u�}�X�g�J�b�g���C���v��u�}�X�g�J�b�g�|�C���g�v���w�肵�Ă��Ă��v�Z���ʂ̊���ʂ��A������ʂ��Ă��Ȃ��B |
| �`�V�|�X�D |
�Ⴆ�u�R�|�J�|�R�v���f���̂悤�ȏꍇ���ꂩ���蒷�̒������̎R���݂̂��擾���Čv�Z���A�����͖������܂��B
�]���Ċ��蒷�̒Z�����̎R���Ɂu�}�X�g�J�b�g���C���v��u�}�X�g�J�b�g�|�C���g�v���w�肵�Ă��Ă���������܂��B |
| �@ |
|
| �p�V�|�P�O�D |
�������ɂ�銊��͂��������Ă��邪�A���̑������̎戵���ɂ��ďڂ��������Ăق����B |
| �`�V�|�P�O�D |
���}�̂悤�ɒ����������郂�f���ł͑������i�Ð����j�ɂ��N���i�����j���[�����g���l�����܂��B
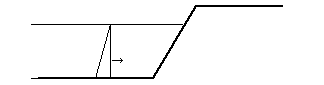
���̑��ɐ��ʂ���͂����ꍇ�A��Ɋ���ʂ̃X���C�X���ɉ��}�̂悤�ɗ������瑤��������p���܂��B
���u���y����v�̏ꍇ�͐��ʂ̓��͕͂s�v�ł����A���͂���Α������͍l������܂��B
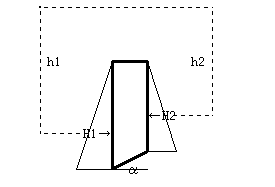
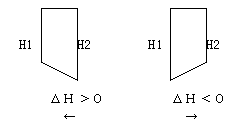
- �������̌����i�����̎����j
- �������̍����g�i��H2�|H1�j�����̏ꍇ
���E���獶�Ɍ������č�p�B
- �������̍����g�i��H2�|H1�j�����̏ꍇ
��������E�Ɍ������č�p�B
- �������v�Z��
���ʂ���͂���ƁA��ɑ������ɂ�銊��͂��l�����܂��B
- ����́i����ʂɍ�p�j
�r���iH2�|H1�jCOS��
- ���胂�[�����g
�l��H2h2�|H1h1
��L���e�X���C�X���ƂɎZ�o���A�S�X���C�X�������v���܂��B
����ʂ̗��[���Ő��������E����Ă��Ȃ��ꍇ�A�������ɂ�鐅���͂��������܂��B
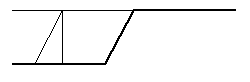
���ʐ��������̂Ƃ��A����~�̏I�[�����ʐ��܂ł���ƍl����Ȃ�·��r���O�ƂȂ�܂��B
�������A�v�Z�͑����̂��ׂ�ʂōs���A�������͎O�p�`���z�̑������i�Ð����j�Ƃ��čl�����邽�߁A���[�����g�͒ނ荇���i���l���O�j�܂����A���ׂ�͈͂�ʂɇ��r���O�ƂȂ�܂��B
���������āA�������ɂ�邷�ׂ�͂̍��v�l���O�ƂȂ�̂́A���ׂ�ʓ��̐��ʂ��~���S�̂x���Ɋւ��č��E�Ώ̂̏ꍇ�݂̂ł��B
- ��R���v�Z��
3-1)�Ԍ������l���̏ꍇ
- ��R�́i����ʂɍ�p�j
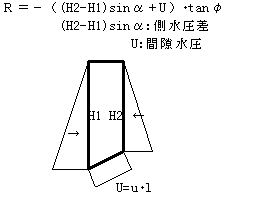
3-2)���́i�L���d�ʁj�l��
���͂��l�������y�̒P�ʑ̐Ϗd�ʃ�'��p���ēy��d�ʂ��Z�o���Ă��邽�߁A�������ɂ���R�͎͂Z�o���Ă��܂���B
���y��d�ʂv�f�����߂�ہA�u��'����sat�|��w�v�ɂ��A �u�|�i���gsin���{U�j�v���̐����́A���ɉ�������Ă���B
�����ʂ����x���ł���i�������̗L���Ɋւ�炸�j�A�Ԍ������ōl�������ꍇ�ƕ��́i�L���d�ʁj�ōl�������ꍇ�Ƃł͈��S���͓����ɂȂ�܂��B�i���ɂ��̌��ؗ�������܂��B�j
�@���ʂ������i�y���j�̏ꍇ
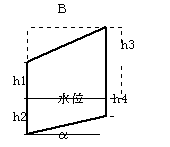
�P�j��R�͂ɂ���
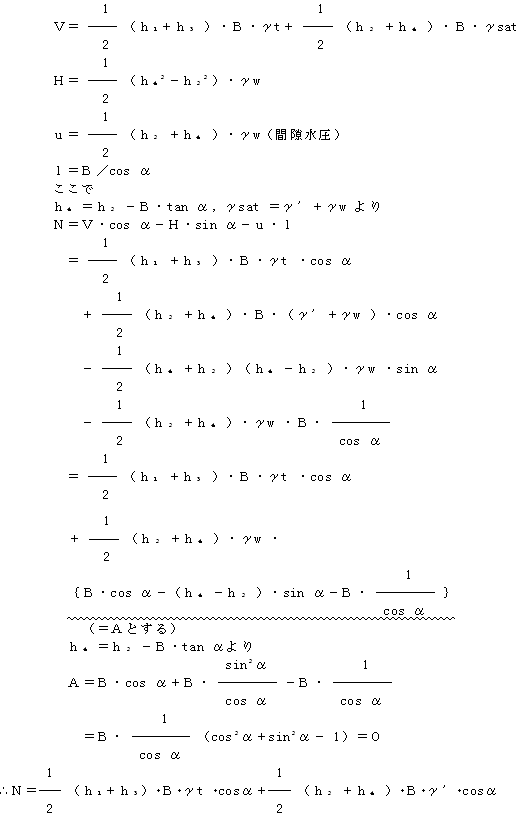
�Q�j���ׂ�͂ɂ���

�A���v�Ζʂ̏ꍇ
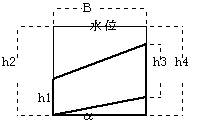
�P�j��R�͂ɂ���
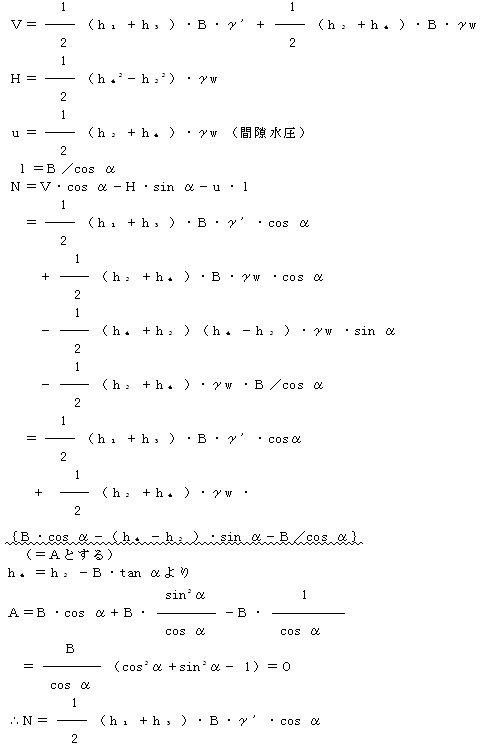
�Q�j���ׂ�͂ɂ���
���������ĕ��́i�L���d�ʁj�ōl�����ꍇ�Ɠ������Ȃ�B
�������ɂ̓v���O�����̓��������Ƃ��ĕ��͂ōl�����ꍇ�ƊԌ������ōl�����ꍇ�Ƃł͊���p�̎������قȂ�܂����i���L�j�A�v�Z���ʂɉe�����o��قǂ̈Ⴂ�͂���܂���B
- ���͂̏ꍇ

- �Ԍ������̏ꍇ
�e�X���C�X�d�S�����W�̊���ʂł̖@�������Ƃ���B
|
| �@ |
|
| �p�V�|�P�P�D |
�n�k���̊����͂ɂ��N�����[�����g���N�����[�����g�����炷�l�Ȍ��ʂɂȂ��Ă���B�d�ɂ�郂�[�����g�Ɠ������ɂȂ�̂ł͂Ȃ����B |
| �`�V�|�P�P�D |
���߂ɖ{�\�t�g�ł́u���������͂̕����́A���ׂ�����ɉ����ăv���O���������Őݒ肵�܂��B�v�Ƃ��������ɂ��Đ������܂��B
�y���u���b�N�f�[�^�̒��ɁA�n�k���v�k�x�̕�W�����̓��͂�����A���͂����v�k�x�i�j���A�j���j�ɑ��āA�i���E�j���A���E�j���j�Ƃ��Ċe�n�w���ɐv�k�x��ω������邱�Ƃ��������Ă��܂��B
�u���ׂ�̕����ɉ����āv�Ƃ́A
�@�@�@�@�@�@�@�@�@�����O�̎��ɂ́A���ׂ�̕����Ɠ��������ɍl������
�@�@�@�@�@�@�@�@�A�����O�̎��ɂ́A���ׂ�̕����Ɣ��Ό����ɍl������
�Ƃ����������Ӗ����Ă��܂��B
����ł́u���ׂ�̕����v�Ƃ͉�����Ɍ��肵�Ă���̂��Ƃ����܂��ƁA�w���ׂ�~�̊J�n�ʒu�ƏI���ʒu�̂x���W�̕W�����݂āA����������Ⴂ�������ׂ�̕����Ƃ���x�Ƃ������f�����Ă��܂��B
���̂悤�ȏ����̒��ŁA�������͂����肵�Ȃ��ꍇ���A���ׂ�~�̊J�n�ʒu�ƏI���ʒu�̂x���W���������ꍇ�A���Ȃ킿�A�t���b�g�Ȓn�\�ʏ�̂��ׂ�~�̏������������܂��B�i���}�j

�܂�A�d�ɂ�蔽���v���ɂ��ׂ肪�������Ă���ɂ��S��炸�A�����͂ɂ͂���ɔ�������悤�ɁA���v���ɍ�p���Ă���A���ׂ�̕����ɉ����Ă��Ȃ����ʂɂȂ��Ă���킯�ł��B�t���b�g�Ȓn�\�ʂł��ׂ�~�����������ꍇ�A���Ȃ킿�w���ׂ�~�̊J�n�ƏI���̕W�������O�̏ꍇ�́A�v���O�������Ŏ��v���ɂ��ׂ�~�������������̂Ƃ��Ĉ���I�ɏ���������x�Ƃ����̂��d�l�ɂȂ��Ă��܂��B���ׂ�̕����̒�`�Â��ɖ�肪����̂ł͂Ȃ����Ƃ����٘_�����낤���Ǝv���܂����A�\�߃t���b�g�Ȓn�`��ł��ׂ�����������ꍇ�ɂ́A�@
�@�@�@�@�@�@�@�����͂����v���i�E�����j�ɍl������ꍇ�ɂ̓����O�Ƃ���B�@
�@�@�@�@�@�@�A�����͂��v���i�����E�j�ɍl������ꍇ�ɂ̓����O�Ƃ���B
�Ƃ������͂Ő�����}���ĉ������B���A�O�q�̂��ׂ�����̒�`����n�\�ʂɎ�̌��z�����������Ƃł�����͉\�ł��B
|
| �@ |
|
| �p�V�|�P�Q�D |
�͂��ȓy��`������_�ōŏ����S�������܂��Ă��܂��B���̕������v�Z�Ώ۔͈͂���͂������@�͂Ȃ����B |
| �`�V�|�P�Q�D |
�u�v�Z���@�̐ݒ�v�́u�ѕЊ�����������v�ɂ����āA
���w���w���|�w�Ƃ���ƁA���������w�Ƃ�����w�͌v�Z�̑Ώۂ���͂�����܂��B
�@�@�w'�F����ʂƒn�\�ʂƂ̌�_�w���W�i�I�_�j
�@�@�w �F �V �i�n�_�j |
| �@ |
|
| �p�V�|�P�R�D |
���S����͂̔�ŋ��߂邱�Ƃ͉\���B |
| �`�V�|�P�R�D |
�{�v���O�����ł͊���ʂ��u�C�ӌ`��v�̍ۂ́A���S����͂̔�ŋ��߂Ă��܂����A�P�~�y�ѕ������ׂ�̏ꍇ�̓��[�����g�̔�Ōv�Z���Ă��܂��B
�A���A�v�Z���ʂ́u�����͂ɂ�銊��́v�Ɂu����͌v�v���A�܂��u��R�́i���̂R�j�v�ɒ�R�͏W�v�l�q�����ꂼ��\���A�o�͂��Ă��܂��̂ŁA�����̒l����͂̔�ň��S�������߂Ă���������Ζ{�v���O�����ł��K�p�\�ƍl���܂��B |
| �@ |
|
| �p�V�|�P�S�D |
�P�~���ׂ�̌��E�ʂ̌v�Z���ʂɂ����āu�������[�����g�^���a������́v�ɂȂ��Ă��Ȃ��B |
| �`�V�|�P�S�D |
���S����͂̔�ŋ��߂��ꍇ�ƃ��[�����g�̔�ŋ��߂��ꍇ�̈Ⴂ�͈ȉ��̂悤�ɂȂ�܂��B
- �͂̔�
- �e�����q�c�^�r�c
�q�c�F����ʏ�̒�R�͂̑��a
�r�c�F����ʏ�̊����͂̑��a
�@�q�c�����o�bi�ki�{�i�vi'�{�����vi�jcos��i�|�����visin��i�|�ti�|���ti�ptan��i
�@�r�c�����o�i�P�{�����j�visin��i�{�����vicos��i�p�{�rP
- ���[�����g�̔�
- �e�����l�q�^�l�c
�l�q���q�c�~��
�q�c�F����ʏ�̒�R�͂̑��a
�@�@���F����~�̔��a
�l�c�����o�i�P�{�����j�vi����i�{�����vi����i�p�{�lP�{�lw
������
�vi�F�X���C�X�̑S�d�ʁi��t�A��sat��p����j(tf/m)
��i�F�X���C�X�̊���p�i�x�j
����i�F�X���C�X�d�S�Ɗ���~���S�̐�������(m)
����i�F�X���C�X�d�S�Ɗ���~���S�̉�������(m)
�����A�����F�v�k�x
�rP�F�d���N����(tf�j
�lP�F�d�ɂ��N�����[�����g(tfm)
�lw�F�������i�Ð����j�ɂ��N�����[�����g(tfm)
���������āu����́v�͊���ʏ�ł̕]���ł���̂ɑ��A�u�������[�����g�v�̓X���C�X�̏d�S�ʒu�Ɗ���~���S����̋����ł̕]���ł��邽�߁u�������[�����g�^���a������́v�Ƃ͂Ȃ�܂���B
�����펞�i�n�k�������͂Ȃ��j�Ő��ʂ����x���̏ꍇ�i���������ʂƂ��ׂ�ʂ̎n�I�_�̍����������j�A�����������E�����̂Ō��ʓI�ɂق�
�u�������[�����g�^���a������́v
���������܂��B
|
| �@ |
|
| �p�V�|�P�T�D |
�i�q�_���S���F�u�|�v�A�u0.00�v�A�u999.99�v�̈Ⴂ�B |
| �`�V�|�P�T�D |
�u�|�v�F���S�������̏ꍇ
�i�ʏ�A�l�����܂���Ńf�[�^�������肭�������B�j
�u0.00�v
�@�@�@��R���[�����g���O�D�O�ƂȂ�ꍇ�i�S�w�̂��A�Ӂ��O�D�O�j
�@�@�A�v�Z�\�Ȃ��ׂ�~�����݂��Ȃ��ꍇ
�i�u��́v���́u�i�q�v�ɂ��Ă��v�Z�̑ΏۊO�ƂȂ��Ă��܂��B�j
�u999.90�v�F���S��������Ȃ��傫���ꍇ�B�������͊ȈՃr�V���b�v�@�Ŏ����ł��Ȃ������ꍇ�����ꂼ��Ӗ����܂��B
|
| �@ |
|
| �p�V�|�P�U�D |
�i�q���`���Ă���ɂ��S�炸�i�q�_���S�����o�Ȃ��B |
| �`�V�|�P�U�D |
�u�v�Z���e�̐ݒ�v�Łu�K�v�}�~�͌��E�ʁv���u����v�ɂ����ꍇ�A�}�~�͂��ő�ƂȂ���E�ʂ��������A���S���ŏ��̌����͍s���܂���B�i��`���ꂽ�i�q�_��ɂ͊e���S���̑���Ɂu�i�q�_�}�~�́v��\�����A�u���ʕ`��v�́u�i�q��_�̊m�F�v�Ŋi�q�_���Ƃ̊m�F���s���܂���B�j
�}�~�͂��ő�ƂȂ���E�ʂ̌����ƈ��S���ŏ��̌����͓����ɂ͂ł��܂���̂ŁA��L�̏ꍇ�́u�K�v�}�~�͌��E�ʁv���u���Ȃ��v�Ƃ��čČv�Z���Ă��������B |
| �@ |
|
| �p�V�|�P�V�D |
���E�ʂ̌v�Z���ʂ̍ŏ����S���e�����A�e�i�q�_�̂e�����Q�Ƃ��Ă���������Ȃ��B |
| �`�V�|�P�V�D |
���L�Q���ڂ����Ɂu����v�������͕Е��̂݁u����v�Ƃ����ꍇ�A�K���������E�ʌv�Z���ʂ̂e�����i�q�_��ɂ���Ƃ͌���܂���B
- �����S���̌v�Z�u����v
�e�i�q�_�y�ъe�i�q���S�_���ΏہB
- ���E�~�̎����ǐՁu����v
�����ǐՂ̍l�����ɏ]���i�u���E�ʂ̎����ǐՌv�Z�v�Q�Ɓj�e�i�q�_�y�т���ȊO���ΏہB
|
| �@ |
|
| �p�V�|�P�W�D |
�����ǐՌ��ʂ̂es �̕����i�q�_�es ���傫���Ȃ�B
�����ǐՔ͈͂Ɗi�q�͈͂�Ƃ��čŏ����S�������߂�ƈȉ��̌��ʂƂȂ����B
- �����ǐՌ��ʁ@�@�es ��1.83
- �i�q�_���S���@�@�es ��1.75
- �����S���̌��ʁ@�es ��1.72
|
| �`�V�|�P�W�D |
�i�q�_���S���͊e�i�q�_��̈��S���̒�����ŏ����S���𒊏o���邾���ł����A�����ǐՂⓙ���S���̌v�Z�͂��ꂼ�ꎟ�̂悤�ɍs���A�ŏ����S�����������Ă��܂��B
- ���E�ʂ̎����ǐՌv�Z
�ǐՔ͈͓��ɂ����ē���̃��C����̈��S���ŏ��_�����������A���ɂ��̃��C����̈��S���ŏ��_�ƒ������郉�C����ł̈��S���ŏ��_�����߂�Ƃ������������J��Ԃ����Ƃɂ��S�̂ł̈��S���ŏ��_��ǐՓI�ɋ��߂܂��B
�i�u���E�ʂ̎����ǐՌv�Z�v�Q�ƁB�j
- �����S�����i�R���^���C���j�̎Z�o
- �i�q�̌�_��̈��S�����v�Z���܂��B�i���`���j
- �i�q�̒��S�̈��S�����v�Z���܂��B�i���j
- �P�`�W�̐����ɑ��ăR���^���C���̑ΏۂƂȂ���S���� ���������[�̈��S���̊Ԃł���A���̈ʒu����ŋ��߂܂��B�i�}�����j
- �P�̊i�q���ɂł����S�̎O�p�`�����Ɍ��Ă����A������łȂ��Ő����̃f�[�^���쐬���܂��B
- �S�Ă̊i�q�ɑ��ē��l�̏������s���܂��B
���u�����v���u�����S���v�ŕ\������Ă�����S���i�ő�T�R�j
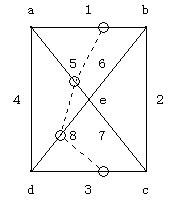
���ʂɕ\�������ŏ����S���es �͏�}�̗�ʼn]�����A���A���A���A���̂T�ӏ��i�S���ƒ��S�j�̒����璊�o���ꂽ�l�ł���A����̂es
�͒��o�ΏۂƂȂ��Ă��܂���B�i�T�ӏ��ȊO�͌v�Z���Ă��܂���j
�ȏ�̂悤�ɁA�����ǐՌv�Z�������S���̌v�Z���������@���K���������\�Ȃ킯�ł͂Ȃ��A�ǂ����Ă��������ꂪ�����A�{���̃P�[�X�̂悤�Ȍ��ʂɂȂ�ꍇ������܂��B
���������Ĕ�r�I�]�܂����v�Z���@�Ƃ��ẮA
- �i�q�͈͂��L���͈͂ő傫�������ݕ����狷���͈͂ŏ����������ݕ��ւƏ��X�Ƀf�[�^��ς��Ă����܂��B���A�K�v�ɉ����ē����S���̌v�Z���s�����S���̕��z�����o�I�ɂ������Ă����܂��B
- �P�̍�Ƃň��S�����������Ȃ�Ƃ����������x�i�荞��A������ǐՔ͈͂Ƃ������ǐՂ̌v�Z���s���čŏ����S�����X�ɍi�荞�݂܂��B
|
| �@ |
|
| �p�V�|�P�X�D |
�}�X�g�J�b�g���C�����`�����ɂ��S��炸�ʂȉӏ��ōŏ����S�������܂�B |
| �`�V�|�P�X�D |
�{�v���O�����ł̓}�X�g�J�b�g���C����}�X�g�J�b�g�|�C���g���w�肵���ꍇ�́A���Ȃ��Ƃ����ꂩ�����ʂ邷�ׂ�ʂ݂̂����S���v�Z�̌����Ώۂɂ��܂��B���������Ĉ�ʂɌ��E�ʂ̌v�Z���ʂɂ͂�����ʂ邷�ׂ�ʂŌ��ʂ�\�����܂��B
�{���̏ꍇ�Ⴆ�Ή��}�̂悤�ȏꍇ���l�����܂��B
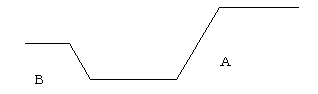
�{�v���O�����ł͂��ׂ蒷�̑傫������D�悵�i�`���a�j�a���̂��ׂ�ʂ͌v�Z�̑ΏۊO�ƂȂ�܂��B���̂��߉��ɂa�����u�}�X�g�J�b�g���C���v�Œ�`���Ă��Ă��A���ʓI�Ɂu�}�X�g�J�b�g���C���v���������̂ƌ����܂��B
��P�j�\�ł���Βn�\�ʂ̓ʉ����Ȃ��������Ƀ��f��������B
��Q�j�a����肽���ꍇ�A�`�����u�v�Œ�`����B
�@�@���a���݂̂��܂��B
|
| �@ |
|
| �p�V�|�Q�O�D |
�C���t�F���j�E�X�@�Ōv�Z������@�B |
| �`�V�|�Q�O�D |
��ʂɊȈՕ����@�������̓t�F���j�E�X�@�Ƃ͎������w���܂��B
�e�������i�����{�i�vcos���|�t�jtan�Ӂj�^���vsin��
����������ʂ̐����Ɛ����p���}�ȃX���C�X�ł́A�u�vcos���|�t���O�v�ƂȂ�ꍇ��������̂Łu�vcos���|�t�v���v'cos���i�v�F�X���C�X�L���d�ʁj�ɒu�������������C���t�F���j�E�X�@�ƌĂт܂��B
�e�������i��'���{�i�v'cos��tan��'�j�^���vsin��
�@�@�@ �i�w�Ζʂ̈����͓���x�y���H�w��@P48�`P49�j�@�@
�@�@�@�i��'�A��'�F�L�����͕\���̋��x�萔�j
�{�v���O�����ł��Ԍ������t���l�����u�vcos���|�t���O�v�ƂȂ�ꍇ�́A0.0�ɂ��Ă��܂��B
�{���̏ꍇ�A�u�j���v���u�L�����͖@�v�Ƃ��u���̎戵���v�ɂ����āu�Ԍ������t�v���u0.0�v�Ƃ����͂Ƃ��čl���i���̈�������sat�|��w�A�������̓�'�j�Ƃ���ΏC���t�F���j�E�X�@�ɂČv�Z�ł���ƍl���܂��B�@ |
| �@ |
|
| �p�V�|�Q�P�D |
�n�\�ʂ܂ł̐��ʂ�����A�_���̕������Ő��ʂ��}�~�����鎞�̍l�����B |
| �`�V�|�Q�P�D |
���L�A���ꂩ�̕��@�Ōv�Z����悢�Ǝv���܂��B
�u���Z����� �v���Ԍ������̌v�Z�ɂ����ē��|�e���V��������C�ӂɓ��͂��Ȃ��ꍇ�A�����ʼn����ɓ��͂��ꂽ���̂Ƃ��Čv�Z���܂��B
�܂藼�P�[�X���A�Z���ʂƊ���ʂƂ̐������ŊԌ��������v�Z����̂Łu���̎戵���v�ȂǑ��̏�������v�����Ă����A����̕��@�ł��v�Z���ʂ͓����ɂȂ�܂��B
�i�u���Z����ԁv�œ��|�e���V��������C�ӂɓ��͂���ƌ��ʂ͕ς��܂��B�j
�i�u���Z����Ԃ̍l�����v�A�u���ʋ}�~�����̍l�����v�Q�Ɓj |
| �@ |
|
| �p�V�|�Q�Q�D |
�u�ȈՂa�����������v�Ɓu�a�����������v�̑���ɂ��āB |
| �`�V�|�Q�Q�D |
�X���C�X�ԗ́i�����͂u�A�����͂g�j���l�����������͕��@�u�a�����������v�̂����u�u���O�D�O�v�Ƃ�����̂��A�u�ȈՂa�����������v�ƌĂт܂��B
�{�v���O�����ł́u�ȈՂa�����������v���T�|�[�g���Ă��܂��B
�T�v�͈ȉ��̒ʂ�ł��B
- �����Őݒ肳��Ă�����S���e�r�O�̏����l�i=1.0�j�����R�͂����߂�B
- ��R�͂ɔ��a���悶�Ē�R���[�����g�����߂�B
- �ʓr���߂��������[�����g�Ə�L�̒�R���[�����g������S���e�r�P�����߂�B
- �e�r�P�|�e�r�O��X.XXX
X.XXX�F�u�v�Z���e�̐ݒ�v�ɂ�����u�ŏ����S���̐��x�v
- �e�r�P��V���ȏ����l�Ƃ��čēx�A��R�͂����߂�B
�ȉ��A��������������܂�2)�ȍ~���J��Ԃ��B
�u�e�r���{�P�|�e�r����X.XXX�v
�i�ڂ����Z�����́u�a�����������̊ȈՖ@�v���Q�Ƃ��ĉ������B�j
���j
��L�v�Z�ɂ����Č��ʓI�Ɏ����ł��Ȃ������ꍇ�́u�i�q�_���S���v�̕\�Ɂu999.90�v�ƕ\������܂��B
���̎��̑�Ƃ��Ắu�ŏ����S���̐��x�v��傫�����čČv�Z���Ă݂鑼����܂���B
|
| �@ |
|
| �p�V�|�Q�R�D |
��R�́|����͐}�Ƃ͉����B�܂����̌����ɂ��āB |
| �`�V�|�Q�R�D |
�u��R�́|����͐}�v�Ƃ́A����́i�s�j�����R�́i�q�j�������������l�i�傫���j���A�ΏۂƂ��Ă��銊������犊��~���S�����̐���ɕ����Ж��Ƀv���b�g�������̂ł��B
����͂���R�͂���Ȃ�i�s���q�j�ꍇ�́A������̓������Ȃ킿�~���S���Ƀv���b�g���A��R�͂���Ȃ�i�q���s�j�ꍇ�͊�����̊O���Ƀv���b�g���܂��B
�܂�u��R�́|����͐}�v�̌����Ƃ��ẮA��R�́|����͐���������������ɂ���Έ����̈�A�O���ɂ���Έ��k�̈�ł��邱�Ƃ��킩��܂��B
����ɂ��̐}����}�~�Y��ݒu����ʒu�Ƃ��āA��R�͂̕����傫���i��R�́|����͐���������̊O���ɂ����ԁj�A���������̓y��肪�[���ɂ���j�N����ɂ����ʒu�������ł�����̂ƍl���Ă��܂��B
�Ȃ��A���̒�R�́|����͐��������������Ȃ����͐ݒ�ł���悤�ɂ��Ă��܂��B�s�v�Ɣ��f���ꂽ�ꍇ�͎��̎菇�Őݒ肵�Ȃ����Ă��������B
�u�`����e�m�F��ʁv���A��̍�������e�ݒ�A�X�P�[���ݒ�A�X�P�[���m�F���̏����I����������܂��B���̒��̓��e�ݒ�����N���b�N����ƁA�����Ɂu��R�́|����́v����E���Ȃ��̐ݒ肪����܂��B������u���Ȃ��v�ɂ��܂��B�����ɕs�v�ƍl�����鍀�ڂ����������u���Ȃ��v�ɂ��āu�ݒ�I���v���Ă��������B |
| �@ |
|
| �p�V�|�Q�S�D |
�u���ׂ��R�͐��v�̈Ӗ��Ǝg�p�ړI�B |
| �`�V�|�Q�S�D |
��R�́i�q�j�̒l���A�ΏۂƂ��Ă��銊��ʂ���Ƃ��ĕ����Ж��Ƀv���b�g�������̂ł��B
�q���O�̏ꍇ�i�����łO�Z�b�g�j�A�y�тq���O�̏ꍇ���ׂ����ɒ�R�͂��v���b�g���܂��B
�q���O�̏ꍇ�A���ׂ���̊O���ɒ�R�͂��v���b�g���܂��B |
| �@ |
|
| �p�V�|�Q�T�D |
�~�E�����̂e���̋��ߕ��B |
| �`�V�|�Q�T�D |
 |
| �@ |
|
| �p�V�|�Q�U�D |
�v�Z�i�q����̂̒��ɓ����Ă���ꍇ�A�Ȃ��v�Z���Ȃ��d�l�ƂȂ��Ă���̂��B
�@�܂��A���ʐ���艺���̊i�q�_�ł̈��S�����v�Z����Ȃ��̂͂Ȃ����B |
| �`�V�|�Q�U�D |
�{�v���O�����́A���ׂ�~���S����̓����邢�͒��������ɂ���P�[�X�ɑΉ����Ă��܂���B�n���[���ʒu�ɉ~���S������~���S����ɂ��ׂ�ʂ����݂���P�[�X�C�Ð������~���S������ɍ�p����P�[�X��z�肵�Ă��Ȃ����߁A���ׂ�~���S�Œ�̂Ƃ��v�Z�O�Ƀ`�F�b�N�������A�i�q�̂Ƃ��Y���ʒu�̊i�_�ɂ��Ă͌v�Z���Ă��܂���B |
| �@ |
|
| �p�V�|�Q�V�D |
�����̒���DOS�œ��l�Ɋi�q�͈͂̕ύX�A�ǐՔ͈͂Ȃǂ̈ړ��͂ł��Ȃ��̂��B |
| �`�V�|�Q�V�D |
DOS�łɁu�����Ŋi�q�͈͂̕ύX�v�@�\������͓̂��͏����܂Ŗ߂��Ċi�q�͈͂̍Đݒ���s���A�Čv�Z�����s����ƌv�Z�ɑ�ώ��Ԃ������邽�߂ł��BWindows�ł̏ꍇ�A�v�Z���Ԃ����Ȃ�Z�k����A�܂����͂��e�ՂɂȂ��Ă��邽�ߎd�l�v�i�K����O���Ă���܂��B
�@�u�ǐՔ͈́v���܂߁A�����̍��W��ύX����ꍇ�́u���W���X�g���́v�ō��W��ύX���ĉ������B |
| �@ |
|
| �p�V�|�Q�W�D |
�ѕЊ�������ɂ��ăf�t�H���g�ł͂O�D�W���ƂȂ��Ă��邪�ǂ̈ʂ�ڈ��Ɍ��߂�Ηǂ��̂��B |
| �`�V�|�Q�W�D |
�ѕЊ������������������Όv�Z���x��������܂����A���̕����Z���ԁC���ʏo�͗ʂ��傫���Ȃ�܂��B
�{�v���O�����ł́A�N�����[�����g�Ɋւ��Ă͕����Ђ��傫���Ȃ��Ă����x��ۂĂ�悤�ɍH�v���Ă��܂����A���ׂ�p���֗^���邷�ׂ�́C��R�͂���ђ�R���[�����g�́A�ѕЊ�������Ɉˑ�����������܂���B�v�Z���f���ɉ����Đݒ肵�Ă��������B |
| �@ |
|
| �p�V�|�Q�X�D |
�C���t�F���j�E�X�@�ɂ��đS���͂ł̉�͉͂\���B |
| �`�V�|�Q�X�D |
�m�v�Z���@�̐ݒ�n�i�ݒ�P�j�́u�j���v�̗L�����͖@�^�S���͖@�̎w��͓y���u���b�N�Œ�`�������C���C�ӂ��Q�Ƃ��Ă��邾���ł��B
�i�ݒ�P�j�́u���̏�ԁv�A�i�ݒ�S�j�́u���̎戵���v�Œ�R�͂̎Z�o���@���`���Ă��������B�u���̏�ԁv�Ɓu�j���v�Ƃ̑g�����ɂ��u���̎戵���v�̐ݒ����g�������̑�����@���v�Z�����̎戵���ɋL�q���Ă��܂��̂ŎQ�Ƃ��Ă��������B |
| �@ |
|
| �p�V�|�R�O�D |
�T���h�R���p�N�V�����p�C���ɂ���b�n�Ղ̉�͂̍ہA���ǑΏۂƂȂ�y���̒P�ʑ̐Ϗd�ʂ́A�����ȓy���̒P�ʑ�
�Ϗd�ʂ���͂���̂��A����Ƃ����Ǘ��ɂ��v�Z�������Ƃ̕��ϓI�ȒP�ʑ̐Ϗd�ʂ���͂���̂��B |
| �`�V�|�R�O�D |
���͂��ꂽ��t�C��sat�͊���́E���[�����g�Z�o�ɗp���܂��B���̂��߁A���Ǘ��ɂ��v�Z�������Ƃ̕��ϓI�ȒP�ʑ̐Ϗd�ʂ���͂�������K�Ǝv���܂��B
�Ȃ��A�v�Z���͂����������_������ьv�Z���@���T���h�R���p�N�V�����p�C���H�@�ɂ����ǒn�ՂɋL�ڂ��Ă��܂��B�i�v�Z���@�́u���H�y�H
���n�Ց�H�w�j�i�i�Ёj���{���H����j���Q�Ƃ��Ă��܂��B�j |
| �@ |
|
| �p�V�|�R�P�D |
�~�ʊ���̌v�Z���Ɍ����i�q�̕������̈��S�������߂���@�́H |
| �`�V�|�R�P�D |
�u�v�Z���@�̐ݒ�v���u�ݒ�R�v�Łu�v�Z�o�߃t�@�C���̏o�́v��I�����ĉ�����
���ɂ��A�������銊��ʌ`�u�~�ʁv�̏ꍇ�ɂ̂݁A�����i�q�̊e�l���Z�o���邱�Ƃ��ł��܂��B
�I�����Ă��Ȃ��ꍇ�́A�����錋�ʂ͍ŏ����S���̏ꍇ�݂̂ɂȂ�܂��B |
| �@ |
|
| �p�V�|�R�Q�D |
�T���h�R���p�N�V�����̎����́ihelp�ɋL�ڂ́j����p�x���͉����H |
| �`�V�|�R�Q�D |
����ʂ̊p�x�ɂȂ�܂��B |
| �@ |
|
| �p�V�|�R�R�D |
�S���y�̋��x���������́A�ǂ��l����̂��H�o�T�͉����H |
| �`�V�|�R�R�D |
�u���H�y�H�@���n�Ց�H�w�j�v�́u�T�͂X�߁@�T���h�R���p�N�V�����p�C���H�@�v�ɏ����Ă���܂��B |
| �@ |
|
| �p�V�|�R�S�D |
Sweden�@�Ōv�Z���������A�����@�̎���Fellenius�@��Sweden�@�Ɠ����v�Z�����H |
| �`�V�|�R�S�D |
Fellenius�@�͓��v���O�����ł́u�t�F���j�E�X�@�i�ȕ֕����@�j�v�̂��Ƃł��B
���́u�t�F���j�E�X�@�i�ȕ֕����@�j�v�͂r�����������@�Ɠ������ƍl���Ă��������Ė��͗L��܂���B���̏ڍׂ̓w���v�u�ȕ֕����@�v�ɋL�q���Ă���܂��B
�t�F���j�E�X�@�͂��Ƃ��ƁA�X�E�F�[�f���@�̌v�Z�����̃X���C�X�Ԃ̑����������[���Ƃ����v�Z���ł���A���v���O�����ł́A�Ԍ��������l������ꍇ�A�e�X���C�X���ɑ������ɂ��e�����l�����܂��B�w���v�́u�v�Z���@�⑫�v�����Q�l�ɂȂ���̂Ǝv���܂��B
���̈�Sweden�@�Ɠ����̌��ʂ邱�Ƃ��\�ł��B |
| |
|
| �p�V�|�R�T�D |
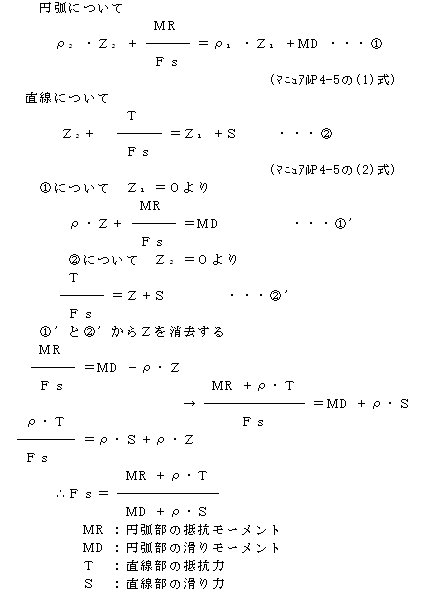
���S��Fs�̎��ɂ��āA�y�H�w�j���ŋL�ڂ���Ă��鎮(A)�Ɩ{�v���O�����̎�(B)�̌`���Ⴄ�̂ŁA(A)=(B)�ɂȂ邽�߂̌v�Z�ߒ���m�肽���B |
| �`�V�|�R�T�D |
(B)�ɂ��ẮA�k�x�A�d�A���������̊e�p�����[�^��(A)�ɂǂ̂悤�ɔ��f����Ă邩�m�Ɏ����Ă���̂ł���A�y�H�w�j�ɂ���ʓI�Ȏ��Ɠ����ł��B�����A�ڍׂɋL�ڂ��Ă��镪�A����ɂ������������邩�Ƒ����܂��B
�ȉ��ɁA���H�y�H�̂�ʍH�E�Ζʈ���H�w�j�i�����P�P�N�R���j�̈���v�Z��P.166�i�펞�j�Ɓu�Ζʂ̈���v�Z�@for�@Windows�v�̎Z���ɂ��Đ������܂��B��������ȕ֕����@�ł��B
�es����{c�EL�{(W�|u�Eb)os���Etan��}�^���iW�Esin��)�E�E�E�E(A)
�es��MR�^MD
�@�@�@��R��{c�EL�{(W�Ecos���|U)�Etan��}�^��(W�E��x)�E�E�E�E(B)
(A)�F���H�y�H�C(B)�F�Ζʂ̈���v�Z
(B)�ł͂�v����h���lp���lw��0.0�Ƃ��Ă��܂��B�܂��A�Ԍ��������l������ɂ́A�u���̎戵���v�Ő��ʈȉ����u�����v�Z�v�Ƃ���K�v������܂��B
(B)���ɂ����āA���q�ɂ��āA�Ζʂ̈���v�Z�ł�U��
�@(1)���͂Ƃ��čl����i���̎戵���ł����O�j
�@(2)�Ԍ������Ƃ��čl����i���̎戵���ł����v�Z�j
�̂Q�Ƃ���̕��@������A
�@(1)�̂Ƃ��A��������������ɍ�p����(u�Eb�Ecos��)
�@(2)�̂Ƃ��A���ׂ�ʂɐ����ɍ�p����(u�EL)
�Ƃ��Čv�Z���܂��B
���H�y�H�̋L�ڎ��͎Ζʂ̈���v�Z��(1)�ɑ������܂��B
����ɂ���
�@�@�@��x��R�Esin���@(R�F���ׂ�~���a)
�ȏ�ɂ��A(B)���́A(A)���̕��q����ѕ���ɂ��ׂ�~���aR���悶�����̂ɂȂ�܂��B(A)�����͂̔��\���Ă���̂ɑ��A(B)���̓��[�����g�̔�ň��S����\���Ă��܂��B |