WebLesson:#10
曲線橋の動的挙動
株式会社 フォーラムエイト 技術サポートグループ |
ランプ橋,取り付け道路との関係から曲線橋は数多く存在する。一見,直線橋に見えても若干曲率が入っているものも多い。
既設の連続桁橋では固定/可動支承が用いられているケースが多く,曲線橋の場合その可動方向は固定支承を有する下部構造の構造中心線を向いているものが多い。この場合,各下部構造の曲げ剛性が橋梁全体の3次元地震時挙動に影響を与えることは言うまでもないが,支承の可動方向・上部構造の面外曲げ剛性も地震時挙動に対して大きな影響を与える。
設計要領第二集(東・中・西日本高速道路株式会社)では,交角が60度程度以上の曲線橋を,動的解析による照査が必要と判断する目安としてよいと記載されており,実務上60度未満の橋梁については,しばしば直線橋として解析されることがある。
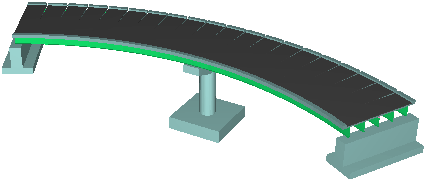
本検討では,交角および上部構造の面外曲げ剛性をパラメータとし,下図に示す2径間連続桁橋に対して非線形時刻歴応答解析を実施し,橋脚に対する損傷度合いを比較することを目的とする。 |
 |
1. 対象橋梁
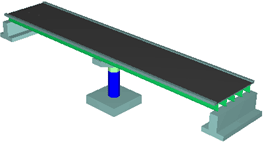
解析対象は交角が異なる下図の4橋とする。さらに,上部構造の面外曲げ剛性を3種類変化させるため,全12ケースとなる。解析は全てUC-win/FRAME(3D)を用いて行う。 |
| CASE-1:直線橋 |
CASE-2:交角θ=30度 |
 |
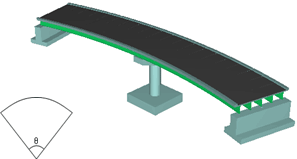 |
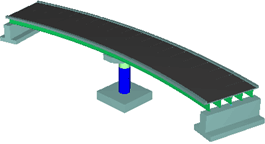
| CASE-3:交角θ=45度 |
CASE-4:交角θ=60度 |
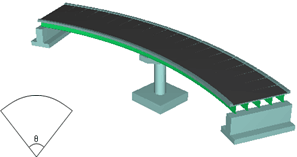 |
 |
図-1. 解析対象構造物概観図 |
橋脚についてはその断面形状による影響が無いよう円柱のT形橋脚とする。形状図を以下に示す。
柱の配筋は,道示Vにならい設計水平震度の下限値khc=0.4czWを満足するように設計しているものである。
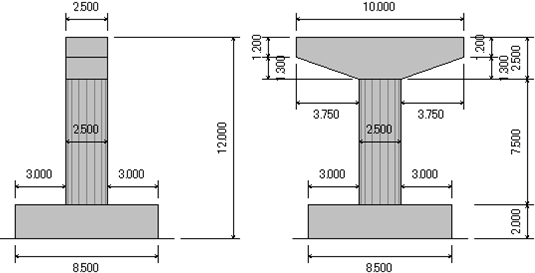
図-2. 橋脚形状図 |
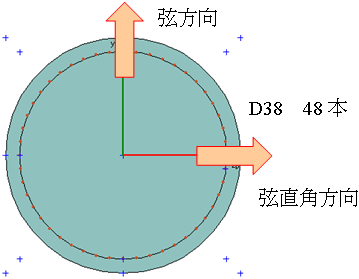
図-3. 柱断面図 |
|
2. 解析条件と解析モデル
CASE-1は直線橋であり,本検討の基本ケースとなるものである。CASE-4は設計要領第二集において,曲線橋として解析する目安となるものである。CASE-2およびCASE-3は上記2ケースの中間モデルである。
いずれも桁長(CL上)60mとし,上部構造の重量は4ケース全て等しい。
なお,地盤種別はI種地盤とし架橋位置はA地域とする。
モデル図を以下に示す。
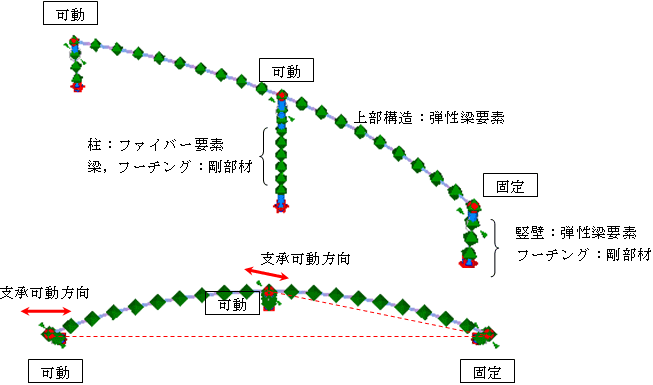
図-4. モデル条件 |
本検討の場合,橋梁は3次元的な挙動を示すことが予想される。このとき,橋脚には二軸曲げが発生する。したがって,二軸曲げを適切に解析できるファイバー要素を用いて解析を行う。
地震波の入力方向は設計要領第二集では「弦方向とその直角方向」,「特に注目する橋脚における主桁軸線に対し接線方向と法線方向」,「特に着目する橋脚断面の主軸方向」が挙げられている。本検討では弦方向,主桁軸線,橋脚の主軸方向は同一であるため,弦方向とその直角方向に地震波を入力することとする。
地震波形は道示V編に準拠し,「II-I-1」のみを作用させる。 |
3. 解析結果
1) ひずみによる損傷程度の把握
本解析はファイバー要素を用いているため,ひずみを指標とした損傷を確認することができる。下図は,全体損傷図である。弦方向および弦直角方向加震双方において柱基部で損傷が発生する結果となった。
弦方向加震では全て同一の損傷であり判別することは難しいが,弦直角方向加震ではθ=30度より大きくなると損傷範囲が広くなる様子が分かる。つまり,若干でも曲線が入ると直線橋の場合と異なる損傷形態を示すことがわかる。 |
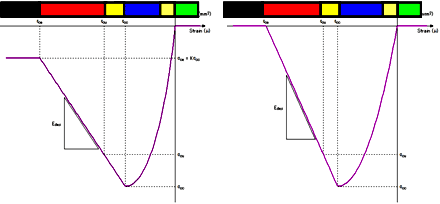
ひずみと損傷レベル |
| |
弦方向加震 |
弦直角方向加震 |
| θ=0度 |
 |
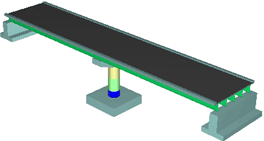 |
| θ=30度 |
 |
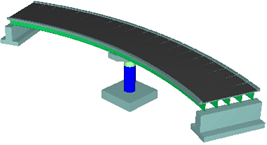 |
| θ=45度 |
 |
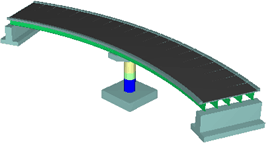 |
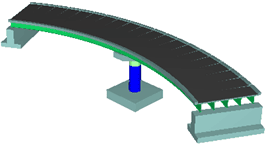
| θ=60度 |
 |
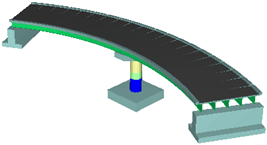 |
図-5. 全体損傷図 |
上部構造の面外剛性について,5主桁を1断面でモデル化し算出した曲げ剛性によるケースを標準ケースとし,標準ケースの1/10,10倍とした,3ケースに対し検討を行う。
図-6は標準ケースの結果である。
いずれの交角および加震方向においても,損傷は軽微なレベルにとどまり,柱基部に集中する。
交角0度では,コア内部まで軽微な損傷が達し,また,側面への損傷が生じない。
一方,交角が大きくなるほど,側面かぶりへの損傷が拡がる。特に,弦直角方向加震において交角最大時(60度)では,かぶり全周にわたって損傷がみられる。 |
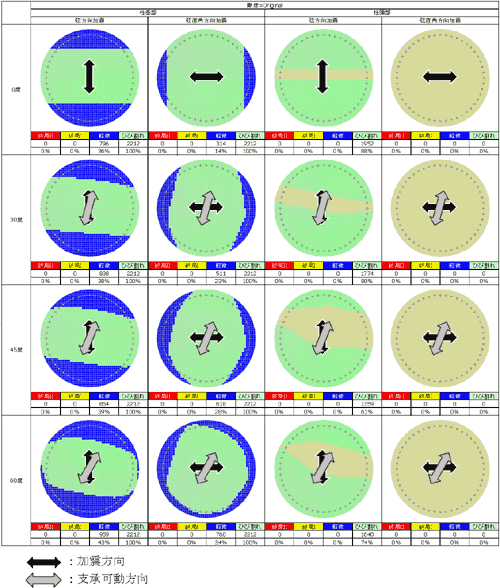
図-6. 断面損傷図(上部構造面外剛度=実断面:標準ケース) |
図-7は上部構造の面外剛性を標準ケースの1/10としたときの結果である。
いずれの交角および加震方向においても,損傷は軽微なレベルにとどまるが,図-6と比べ軽微な損傷を受ける範囲が拡がる傾向にある。
弦方向加震では,交角がわずかに変化するだけで(30度),損傷領域が大きく,全周に拡がる。
弦直角方向加震において,図-6では生じなかった柱頭部への損傷の発生が確認される。しかし,交角0度以外では,交角の違いによる大きな変化はない。 |
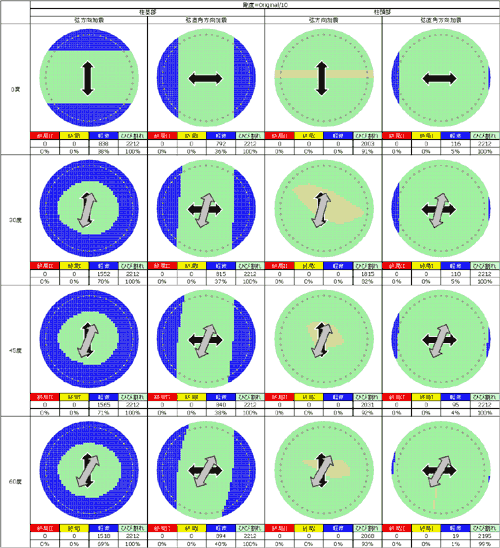
図-7. 断面損傷図(上部構造面外剛度=実断面/10) |
図-8は,上部構造の面外剛性を標準ケースの10倍としたときの結果である。図-6,7と同様,損傷は軽微なレベルにとどまっている。面外への拘束が強くなるため,弦直角方向加震の損傷範囲は図-6と比べ大きく減少する。また,同時に交角の違いによる大きな変化も生じにくくなっている。 |
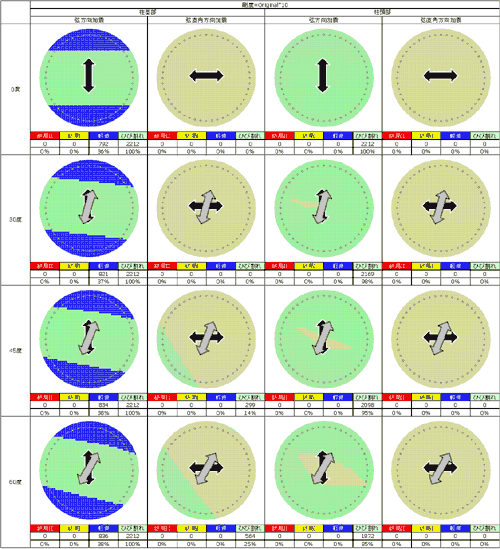
図-8. 断面損傷図(上部構造面外剛度=実断面x10) |
2) 交角および上部構造面外剛性と損傷の関係
交角と上部構造面外剛性,損傷範囲(縦軸)の関係を示したのが下図である。
横軸は上部構造の面外剛性でありそれぞれ1/10(org/10),標準ケース(org),10倍(org*10)を示し,奥軸は交角を示している。また,縦軸は損傷領域の面積比(損傷面積/断面積)を示している。
柱基部の弦方向加震に着目すると,曲線橋で上部構造の面外剛性が小さい場合,損傷範囲が拡がっていることが分かる(図a))。しかしながら,面外剛性が大きくなると交角の大小に影響を受けず,損傷範囲はほぼ一定となる。
一方,柱基部の弦直角方向加震では上部構造の面外剛性が小さくなると交角に大小に関係なく損傷範囲が一定となる(図b))。
柱頭部の弦方向加震ではほとんど損傷は生じない。これは支承可動方向と加震方向がほぼ等しいためと思われる(図c))。柱頭部の弦直角方向加震でもほとんど損傷は生じないが,上部構造の面外剛性が小さくなると若干損傷が発生する(図d))。
支承反力の概念図を図-10に示す。 |
図-9. 交角,上部構造面外剛性,損傷の関係

図-10. 支承反力概念図 |
4. まとめ
4つの交角の異なる橋梁について,上部構造の面外剛性を変えた3ケースに対し,弦方向加震,弦直角方向加震の加震を別々に行った。全て,損傷は軽微なレベルにとどまったが,損傷を受ける範囲について,次の結果となった。
・交角が30度と微小であっても,動的な挙動は直線橋と異なる。
・上部構造の面外剛性が小さいモデルで,弦方向に加震した場合では,柱基部へ与える影響は大きい。
・弦直角方向に加震した場合では,上部構造面外剛性が小さいとき損傷は一定であるが,剛性が大きくなるに従い,交角の影響を受ける結果となった。
・柱頭部では,全てのケースで損傷は軽微であった。
・上部構造の面外剛性が非常に大きい場合,交角の大小は結果にほとんど影響を与えない。
・以上のことから,上部構造の平面線形,橋種,支承条件などにより曲線橋の動的挙動は変化するため,二軸曲げに対応できる非線形梁要素を用いて立体解析を行うことが重要である。
参考文献
[1]設計要領第二集 橋梁建設編,東・中・西日本高速道路株式会社,平成18年4月
[2]道路橋示方書・同解説,社団法人日本道路協会,平成14年3月 |