| New Products |
|
|
●最新版製品価格 |
●リリース 2013年 12月
UC-win 動的非線形解析 |
|
|
| 動的解析セミナー |
CPD |
●開催日 :2013年12月6日(金)9:30〜16:30
●本会場 : 東京本社 品川インターシティA棟セミナールーム
※TV会議システムにて 東京・大阪・名古屋・福岡・仙台・札幌・金沢 にて同時開催
●参加費 :1名様 \18,000 (税別) |
|
H24道路橋示方書V耐震設計編10.2において、許容塑性率μaは、限界状態に相当する変位を降伏変位で割って求めることが条文に規定されています。これを動的照査に適用すると、最大応答変位を降伏変位で割った応答塑性率μがμaを超えていないことを照査することになります。これは単柱式の鉄筋コンクリート橋脚に限定されますが、地震時保有水平耐力法による静的照査と整合します。
従来から構造形式を限定せずに適用可能な曲率による照査や回転角による照査機能がありますが、今回、変位による塑性率照査を行う機能を追加しましたので、桁橋形式の橋梁の動的照査に使用できます。計算式は以下のとおりです。
μ≦μa2 (耐震性能2の照査)
μ≦μa3 (耐震性能3の照査)
ここで、
μ = δmax / δy
μa2 = δls2 / (α2 * δy)
μa3 = δls3 / (α3 * δy)
δmax = δt+h1*θt-δb-h*θb
δls2 = δy+(φls2-φy)*Lp*(h-Lp/2)
δls3 = δy+(φls3-φy)*Lp*(h-Lp/2)
δy = Mls2 / My0 * δy0
φy = (Mls2/My0)*φy0
記号説明;
δt:橋脚天端の水平変位
δb:基礎底面の水平変位
θt:橋脚天端の回転角
h:基礎底面から上部構造慣性力作用位置までの高さ
h1:橋脚天端から上部構造慣性力作用位置までの高さ
φls2:耐震性能2の限界状態曲率
φls3:耐震性能3の限界状態曲率
φy0:初降伏曲率
Mls2:耐震性能2の限界状態曲げモーメント
My0:初降伏曲げモーメント
δy0:初降伏変位(=∫φydy)
Lp:塑性ヒンジ長
α2:耐震性能2の安全率
α3:耐震性能3の安全率
二軸曲げを受ける場合にも対応するため、楕円補間を行います。計算手順は以下のとおりです。
- hの楕円をつくる
- h1の楕円をつくる
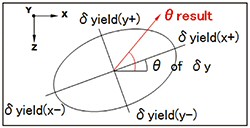
- δyの楕円をつくる(図1)
- δls2の楕円をつくる
- δls3の楕円をつくる
- フレーム計算をする
- 各ステップで次の処理を行う
- 1)天端節点変位から基部節点変位を引いた方向の角度θresultを求める
- 2)θresultの方向でhの楕円を切り取り、その方向のhを求める
- 3)θresultの方向でh1の楕円を切り取り、その方向のh1を求める
- 4)θresultの方向でδyの楕円を切り取り、その方向のδyを求める
- 5)θresultの方向でδls2(δls3)の楕円を切り取り、その方向のδls2(δls3)を求める
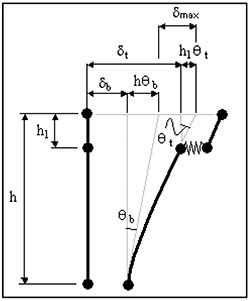
- 6)δmax = δt+h1*θt-δb-h*θb を計算する(図2)
- 7)μ を計算する
- 8)μa を計算する
- 9)安全率μ/μaを求める
-
 |
|
 |
| ▲図1 降伏変位δyの楕円 |
|
▲図2 橋脚躯体の最大 応答変位δmax |
- 各ステップの安全率μ/μaの中から、最大となる安全率とそのときのステップを求める(図3)
- 平均荷重があるときは、各ランの安全率μ/μaを平均する
-
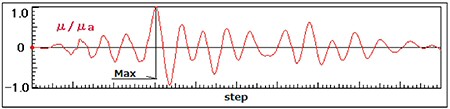 |
| ▲図3 各ステップの安全率μ/μa |
特徴として、1.基礎の回転による水平変位や基礎自身の水平変位を除去して最大応答変位δmaxを求めること、2.各ステップで塑性率の照査を行って最も厳しい結果を最終結果とすること、が挙げられます。 |
H24道路橋示方書V耐震設計編p.122解説文では、鉄筋コンクリート橋脚のM−φ特性を下式で作成する例が示されています。
My = Py(h - Lp/2) ---(解7.3.1)
φy = (δpy/(h-Lp/2))/Lp ---(解7.3.2)
上式は、地震時保有水平耐力法による降伏耐力と降伏水平変位を動的解析用に補正することで静的照査と動的照査が等価になるように配慮されたものです。これは地震時保有水平耐力法が適用可能な構造形式に適用が限定されます。
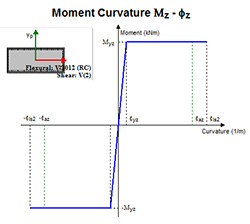
今回、上式によって完全弾塑性型のバイリニアを作成する機能を追加しました(図4)。
弊社製品「震度算出(支承設計)」や「橋脚の設計」からesファイルをエクスポートすると、上式によるM−φ特性が算出されていますが、任意設定なので断面と連動していません。今回より、断面と連動しますので、断面形状や配筋の変更に追随し、M−φ特性も自動更新されます。
断面の形が上下非対称な場合や、圧縮側鉄筋量と引張側鉄筋量が異なる場合など、断面が非対称なときは正側と負側の降伏点が異なるので、原点から正側降伏点を結んだ勾配と原点から負側降伏点を結んだ勾配が一致せず、バイリニア型のM−φ特性が生成できません。今回、以下の要領で補正する処理も追加しました。
 |
|
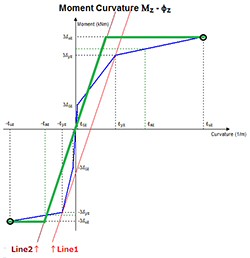 |
| ▲図4 H24道示V-p.122のM−φ特性 |
|
▲図5 M−φ特性の補正(非対称断面) |
- 正側降伏点と負側降伏点をつないだ直線の傾きを第1勾配とする(図5のLine1)
- Line1を原点に移動し、その直線と正側(負側)の耐力を通る水平線とが交差する点を新たに降伏点として補正する
|
鉄筋コンクリート断面の形状をいくつかに限定し、その形状専用の入力と配筋ができる簡易入力を追加しました。形状は、矩形、小判(横)、小判(縦)、円形、I桁、T桁、ダブルT桁、箱桁、円孔ホロー桁です。
複雑な形状は従来からある入力方法「アウトライン→断面→鉄筋配置」で行い、矩形単鉄筋断面などの形状は、この新しい簡易形状入力で行うと入力の手間が減るので便利です(図6)。
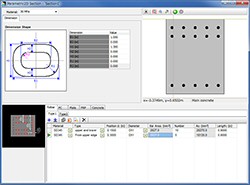 |
| ▲図6 RC断面の簡易形状入力 |
|
IFCは非営利国際組織IAI(International Alliance for Interoperability)が策定及び普及活動を行っている3次元建物情報オブジェクトデータモデルの標準フォーマットです。ソフト間のデータ共有を可能にするCADデータの一種と言えます。
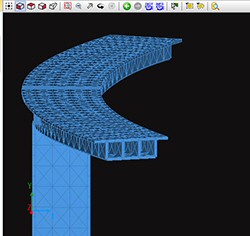
Engineer's Studio®でモデル化されたフレーム要素の任意断面形状、平板要素をIFC形式に変換してエクスポートできます。IFCの対応スキーマバージョンはIFC2X3です。剛体要素、ばね要素、ケーブル要素などの要素は、線分の組合せとしてエクスポートされます(図7,8)。図8は、Karlsruhe
Institute of Technology (KIT)社の無償ソフト「FZKViewer」で読み込んだ様子です。
 |
|
 |
| ▲図7 Engineer's Studio®のモデル |
|
▲図8 IFC形式に対応しているソフトで読んだ状態 |
|
| (Up&Coming '13 晩秋の号掲載) |
 |
|






>> 製品総合カタログ
>> プレミアム会員サービス
>> ファイナンシャルサポート
|








