|
关���їp纤维�v�f�I�͌^���CH29���H桥����书�IV编p.177�\���g为����确计�Z�o钢�؍��Óy桥�r�I终�ǐ����ϗ́C��桥�r������钢�ؗv�f�a���Óy�v�f�C����这��应�͓x-���^��线进�s��线�����́h�h���说�B���C��̓I�͌^�����@�v��G�́B
guān关
yú��
cǎi��
yòng�p
xiān纤
wéi维
yào�v
sù�f
de�I
mó��
xíng�^
hu�
�C
H
2
9
dào��
lù�H
qiáo桥
sh�
fāng��
shū书
de�I
V
biān编
p
.
1
7
7
biǎo�\
sh�
�g
wèi为
le��
jīng��
què确
jì计
suàn�Z
chū�o
gāng钢
jīn��
hùn��
níng��
tǔ�y
qiáo桥
jiǎo�r
de�I
zhōng终
jú��
shuǐ��
píng��
nài��
l�
�C
jiāng��
qiáo桥
jiǎo�r
fēn��
gē��
chéng��
gāng钢
jīn��
yào�v
sù�f
hé�a
hùn��
níng��
tǔ�y
yào�v
sù�f
�C
gēn��
jù��
zhè这
xiē��
yīng应
l�
dù�x
-
shī��
zhēn�^
qū��
xiàn线
jìn进
xíng�s
fēi��
xiàn线
xìng��
fēn��
xī��
�h
�h
bèi��
ji�
shuō说
�B
k�
sh�
�C
jù��
tǐ��
de�I
mó��
xíng�^
hu�
fāng��
fǎ�@
méi�v
bèi��
chù�G
mō��
�B
�����ŁA���������J���@�l�y�،������̓y��������4262���u�S�R���N���[�g���r�̒n�k�����E��Ԃ̕]����@�Ɋւ��錤���v�i����25�N3���j���Q�Ƃ��܂��B���Y�����Ƀt�@�C�o�[�v�f��p������͎���Ƌ�̓I�ȃ��f�������@���L�ڂ���Ă��܂��B�����ł́A���̉�͎�����Q�l�ɂ����ݒ����Љ�����܂��B
�ݓߗ��C�Q�ƍ�������开发�@�l�y�،������I�y��资����4262���u�L关钢�؍��Óy桥�r�I�n�k������态�I评����@�I�����v(����25�N3��)�B该资����记载���g�p��纤���f�I���͎���a��̓I�͌^�����@�B��这���C��绍�ꉺ�Q�l���ߘ���͎���I设���q�B
zài��
n�
lǐ��
�C
cān�Q
zhào��
guó��
l�
yán��
jiū��
kāi开
fā发
fǎ�@
rén�l
tǔ�y
mù��
yán��
jiū��
suǒ��
de�I
tǔ�y
yán��
zī资
liào��
d�
4
2
6
2
hào��
�u
yǒu�L
guān关
gāng钢
jīn��
hùn��
níng��
tǔ�y
qiáo桥
jiǎo�r
de�I
dì�n
zhèn�k
xiàn��
zh�
zhuàng��
tài态
de�I
píng评
ji�
shǒu��
fǎ�@
de�I
yán��
jiū��
�v
(
píng��
chéng��
2
5
nián�N
3
yu�
)
�B
gāi该
zī资
liào��
zhōng��
jì记
zǎi载
le��
shǐ�g
yòng�p
guāng��
xiān纤
yuán��
sù�f
de�I
fēn��
xī��
sh�
l�
hé�a
jù��
tǐ��
de�I
mó��
xíng�^
hu�
fāng��
fǎ�@
�B
zài��
zhè这
lǐ��
�C
ji�
shào绍
yī��
xi�
cān�Q
kǎo�l
le��
n�
ge��
ji�
xī��
sh�
l�
de�I
shè设
dìng��
l�
zi�q
�B
图1�Ɏ����悤�ɁA�P�����S�R���N���[�g���r�ɑ��Ċ���t�@�C�o�[�v�f�Ƃ��܂��B�v�f���͑Y���q���W��Lp�Ƃ��܂��B
�@图1�����C��对��单����钢�؍��Óy桥�r�C���为纤维�v�f�B���f长�x为�Y��铰链长Lp�B
图1桥���͌^
tú图
1
qiáo桥
zhù��
mó��
xíng�^
�t�@�C�o�[�f�ʂ́A�R�A�R���N���[�g���i���F�����j�Ƃ��Ԃ�R���N���[�g���i�F�����j�ɕ����ă��b�V���������܂��i图2�j�B
纤维�B�ʕ�为�j�S���Óy�����i�K�F�����j�a����Óy�����i蓝�F�����j进�s㤏��i图2�j�B
图2��纤�f��㤊i����
tú图
2
guāng��
xiān纤
duàn�f
miàn��
wǎng�
gé�i
fēn��
gē��
�R�A�R���N���[�g�̉��͂Ђ��Ȑ�
�j�S���Óy应�͎��^��线
hé�j
xīn�S
hùn��
níng��
tǔ�y
yìng应
l�
shī��
zhēn�^
qū��
xiàn线
�R�A�R���N���[�g���͉��S�����ʂ��l���ł��܂��̂ŁA�J�e�S�����uHoshikuma�v�Ƃ��A�S�ɂ�鉡�S�����ʂ�ݒ肵�܂��i图3�j�B
�j�S���Óy����为�\�l虑��(侧)�S�����ʁC�c类别��为�uHoshikuma�v�C设��R��钢�ؓI��(侧)�S������(图3)�B
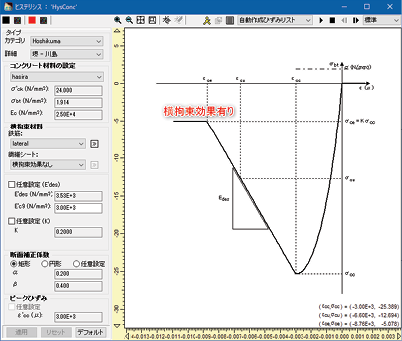
图3�j�S���Óy�I�؉�
tú图
3
hé�j
xīn�S
hùn��
níng��
tǔ�y
de�I
zh�
hu�
xìng��
���Ԃ�R���N���[�g�̉��͂Ђ��Ȑ�
����Óy�I应�͎��^��线
fù��
gài�
hùn��
níng��
tǔ�y
de�I
yìng应
l�
shī��
zhēn�^
qū��
xiàn线
���Ԃ�R���N���[�g�����J�e�S�����uHoshikuma�v�Ƃ��܂����A���S�����Ȃ��A���S���̑̐ϔ䂪0�̏ꍇ�A�ő剞�͌�̉��~���z���Z�o���邱�Ƃ��ł��Ȃ��Ƃ�����肪����܂��B���̂��߁A�y��������4262���ł́A���S���ؑ̐ϔ���\���ɏ����Ȓl�Ƃ���0.05%����͂��ĉ��~���z���Z�o���Ă��܂��i图4�j�B
�浇���Óy��份��c类别��为�uHoshikuma�v,�s过�C�L���S�����C���S�����I��积�䐥0�I��v�C�s�\�Z�o�ő�应�͍@�I���~��x这样�I问题�B为���C�y��资����4262���C��为�[����值输��0.05����为���S������积��计�Z�o���~��x(图4)�B
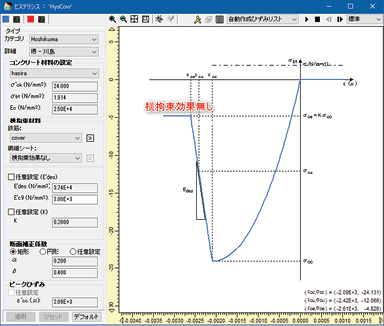
图4����Óy�I�؉�
tú图
4
fù��
gài�
hùn��
níng��
tǔ�y
de�I
zh�
hu�
xìng��
�����ŁA�Q�l�̂��߂ɃR�A�R���N���[�g�Ƃ��Ԃ�R���N���[�g�̃q�X�e���V�X���d�˂Ĕ�r�����图5�̂悤�ɂȂ�܂��B
这���C为���Q�l�j�S���Óy�a��Óy�I�؉d叠��较�I话�C图5变����样�B
图5����Óy�I�؉�
tú图
5
fù��
gài�
hùn��
níng��
tǔ�y
de�I
zh�
hu�
xìng��
�R�t�@�C�o�[�v�f�̂l�|�ӗ�������
��纤���f�IM-��历�j响应
guāng��
xiān纤
yuán��
sù�f
de�I
M
-
��
lì历
shǐ�j
xiǎng响
yìng应
�t�@�C�o�[�v�f�̂l�|�ӗ���������图6�Ɏ����܂��B��r�̂��߂ɁA�l�|�ӓ�����ΐ��ŕ\�����Ă��܂��B�l�|�ӓ����́A���k���̂��Ԃ�R���N���[�g�̉��͕��S���l�����A���������̂��Ԃ�R���N���[�g�ɉ��S�����ʂ��l���������͂Ђ��Ȑ���ݒ肵�ĎZ�o���ꂽ���̂ł��̂ŁA�t�@�C�o�[�v�f�Ə������قȂ�A�P���ɔ�r�ł��܂��A�T�ˈ�v���Ă���ƌ����܂��B
��图6�����o纤维���f�IM-��历�j响应�B为����较�C�p绿�F线�\����M-�ӓ����BM-�ӓ������s�l虑压缩侧�I�浇���Óy�I应��负�S�C��侧�������I�浇���Óy��设��l虑����对�B
|